Trees are able to adapt to changing environmental conditions through modifications in their crown morphology and branch architecture. In light-limited environments, tree structures are mainly optimised to increase light interception. This might have side effects on other properties such as the hydraulic system that determines water conduction and tree reactions to drought events. Given the increasing exposure of forest ecosystems to drought stress it is thus crucial to investigate possible correlations between the crown morphology and branch architecture and drought responses. Our study aimed to compare different crown archetypes and branch characteristics of European beech (Fagus sylvatica L.) in their reaction to drought, which was assessed by measuring tree-ring widths of increment cores sampled at breast height. Using Terrestrial Laser Scanning and Quantitative Structure Models, we explored various crown morphological and branch architectural characteristics of 67 beech trees and identified three species-specific crown archetypes. The crown archetypes and branch variables were contrasted with growth responses using linear mixed models. While productivity levels differed, the negative impact of drought stress on radial growth was consistent across all crown archetypes. Nevertheless, certain branch architectural variables were important predictors for radial growth in drought situations. Specifically, long water conduction paths and many branching nodes along those paths were positively influencing growth. Our results indicate that trees showing these characteristics might have a competitive edge regarding drought-affected radial growth compared to others. They could be promoted through thinning measures, which would allow improving the adaption of existing beech forests in situ to climate change and drought stress.
As place-bound organisms, trees are inevitably exposed to the variable conditions in their environment (Fritts, 1976; Kozlowski and Pallardy, 1997). The growing conditions within a forest stand, for example in terms of light availability and competitive situation, change dynamically over time. As a result of adapting to these conditions, each tree develops an individual structure, aiming to optimise its access to light and other resources, thereby maximizing its growth potential (Horn, 1971; Givnish, 1988; Tilman, 1988; Hutchings and de Kroon, 1994). Tree crown morphology and branch architecture are particularly plastic traits (Jucker et al., 2015), allowing trees to adjust to environmental changes (Canham, 1988; Valladares et al., 2007). Therefore, tree crowns reflect the results of complex interactions of primary and secondary growth processes in response to previous and prevailing environmental conditions (Bayer et al., 2013) and influence present tree functioning and growth (Pretzsch, 2021). This structural and functional relationship between tree crowns and growth is well known and can be traced back to the pipe model theory of Shinozaki et al. (1964), which relates the stem sapwood area to the crown leaf area. Accordingly, several studies found that crown morphology and branch architecture, which represent the leaf area and spatial distribution of leaves, influence tree growth through light absorption and photosynthesis (Ross, 1981; Wang and Jarvis, 1990). Furthermore, branch architecture likely influences hydraulic conduction and therefore tree growth responses to drought stress. When analysing tree growth dynamics, recognizing the significance of crown characteristics is crucial for unravelling the intricate relationships between form, function, and ecological strategies (Laurans et al., 2024).
Since crown-related terminology has not yet been standardised in literature, the following definitions are proposed. Crown morphology is a term that describes the outer characteristics of the entire tree crown that are related to its size and shape, such as the length, volume, or asymmetry of the crown. In contrast, the term branch architecture refers to the inner characteristics of the tree crown that are associated with the branching structure, such as the number of branching nodes, the water conduction path lengths, or branch characteristics.
The adaptions of tree crowns to their environment can be studied by usage of tree allometry, which is a well-established concept relating dimensional traits with morphological or physiological traits (Assmann, 1970; Niklas, 1994). Accordingly, crown morphological characteristics, such as the crown size, can be predicted based on the stem diameter or other factors (Bechtold, 2003; Kershaw Jr. et al., 2016). Similarly, the size of the crown is strongly related to the leaf area, which in turn determines the above-ground resource acquisition and thus radial growth (Fritts, 1976; Mäkelä and Valentine, 2006; Dieler and Pretzsch, 2013). Although trees with large crowns benefit from greater resource access under favourable conditions (Niklas, 1992; Caldwell and Pearcy, 1994), their large leaf area can be disadvantageous during water shortage (Condit et al., 1995; Bennett et al., 2015). This is due to an inherent greater susceptibility to hydraulic failure of large trees (Ryan et al., 2006), higher exposure to radiation and heat, and higher evapotranspirational demands (Bennett et al., 2015), resulting in reduced radial growth (Chen et al., 2017; Chuste et al., 2019).
However, not only crown morphological but also branch architectural characteristics might affect tree growth reactions to drought stress. For example, Früh (1995) and Früh and Kurth (1999) discovered a spatial pattern in leaf-specific conductivity – which represents the hydraulic conductivity at specific points in the branching architecture related to the corresponding leaf area to be supplied – that influences water supply to the leaves, transpiration rates, photosynthesis rates, and the risk of embolism during drought stress. Additionally, the length of the xylem network from roots to leaves affects hydraulic conductance and consequently photosynthesis (Hubbard et al., 2001; Delzon et al., 2004). Rust and Roloff (2002) identified nodes and abscission zones as constriction points for water transport in the branches of mature oak trees, demonstrating that hydraulic conductivity decreases in older trees with longer water transport pathways, which impacts water availability. These findings underscore the potentially pivotal role of branch architecture in tree growth patterns, particularly in response to the challenges posed by drought stress.
So far, the role of crown morphology and branch architecture when investigating the impact on tree growth reactions to drought stress has received limited attention. While some studies have already linked specific crown morphological characteristics of coniferous trees to tree-ring patterns (Pretzsch, 2021; Pretzsch et al., 2022; Ahmed and Pretzsch, 2023), comparable investigations for deciduous tree species are lacking. Although Lebourgeois et al. (2015) addressed the relationship between crowns of a deciduous tree species with radial growth and climate, they defined crown types based on vitality and not based on crown morphology or branch architecture. While the influence of branch architecture on the hydraulic systems, stomatal conductivity, and photosynthetic capacity of trees during drought stress has been documented (Früh, 1995; Früh and Kurth, 1999; Hubbard et al., 2001; Rust and Roloff, 2002; Delzon et al., 2004), these findings have not yet been connected to tree radial growth. In fact, the relationship between crown characteristics and drought-affected tree radial growth remains unexplored for any tree species, representing a significant research gap. Further, a classification of tree crowns into overall crown archetypes, reflecting different crown morphologies and branch architectures, has not been realised before. These crown archetypes could aggregate the effects of various crown characteristic into one factor influencing radial growth under drought conditions. Identifying either an overall crown archetype or certain crown morphological and branch architectural characteristics which are beneficial for the radial growth under drought stress could inform forest management strategies for drought stress adaptation of existing forest stands.
For Central European forests, the European beech (Fagus sylvatica L.) is the most common and important deciduous tree species. It is a highly competitive species, which forms pure stands under optimal conditions and outcompetes all other species through shading (Leuschner and Ellenberg, 2017). The European beech was long considered as a safe tree species choice considering the establishment of forest stands under changing climatic conditions. However, during recent increases in drought event frequency, intensity, and duration, even the European beech was pushed to its limits of physiological survival at many sites (Archambeau et al., 2020; Bigler and Vitasse, 2021; Larysch et al., 2021; Obladen et al., 2021). Drought responses of beech ranged from decreased growth up to tree mortality (Obladen et al., 2021). And, since forests are likely to experience increased drought severity due to climate change (IPCC, 2022), it is important to assess which trees cope better under such conditions. As the mechanisms leading to mortality are not yet fully understood (McDowell et al., 2013; Cailleret et al., 2017), in this study we focus on radial growth reductions, which are easy to measure and can serve as an indicator of a tree's vitality decline towards mortality (Pedersen, 1998; Cailleret et al., 2017). Another important characteristic of the European beech is its high morphological plasticity (Roloff, 2001; Pretzsch and Schütze, 2005), which results in a wide spectrum of crown morphologies and branch architectures as a consequence of adaption to continuously changing environmental conditions (Dieler and Pretzsch, 2013). These adaptions primarily aim to optimise the access to light, which is often the growth-limiting factor in forest stands (Hutchison and Matt, 1977; Tilman, 1988; Muth and Bazzaz, 2003). However, while these crown and branch adaptions may maximise light capture, they may not necessarily be optimal for growth during pronounced drought events.
We therefore aimed to investigate, whether there is an overall optimal crown archetype or specific crown and branch characteristics wherein the negative effects of drought on tree radial growth of European beech are minimised. Given its significance for European forests and its high morphological plasticity, the European beech presents an ideal species to investigate this objective. Using modern remote sensing technologies, we conducted a detailed assessment of the crown morphology and branch architecture, which was then related to radial growth under drought stress.
Our specific hypotheses were as follows.
1. The sample trees can be categorised into crown archetypes, based on information of various crown morphological and branch architectural characteristics, all of which influence the radial tree growth, into one factor. This is why we expect the general level of radial growth to differ between the archetypes.
2. Because the crown characteristics incorporated within the crown archetypes also influence hydraulic conductivity and other aspects relevant to tree drought responses, we expect different degrees of drought effects on radial growth between crown archetypes. Specifically, we expect trees with larger crowns to be more susceptible to drought stress because of their greater susceptibility to hydraulic failure, higher radiation and heat exposure, as well as their higher evapotranspirational demands and losses, due to their large leaf area.
3. Specific branch architectural characteristics influence the tree's hydraulic structure and therefore in particular radial growth under drought conditions. We hypothesise that trees with more branching nodes and longer water conduction pathways have a growth disadvantage during drought stress due to less efficient hydraulic conductivity.
2.
Material and methods
The methodology is based on the precise assessment of the three-dimensional structure of beech trees using Terrestrial Laser Scanning (TLS), a remote sensing technique based on Light Detection and Ranging (LiDAR). Quantitative Structure Models (QSMs) were employed to construct spatial representations of the trees by fitting cylinders to the TLS data, from which crown morphological and branch architectural characteristics can be computed (Disney et al., 2018). Using cluster analysis, the sample trees were categorised into crown archetypes based on these characteristics. The relationship between tree radial growth, measured as tree-ring widths, and the crown archetypes as well as specific crown characteristics was investigated using Linear Mixed Effects Models (LMEMs).
2.1
Study site
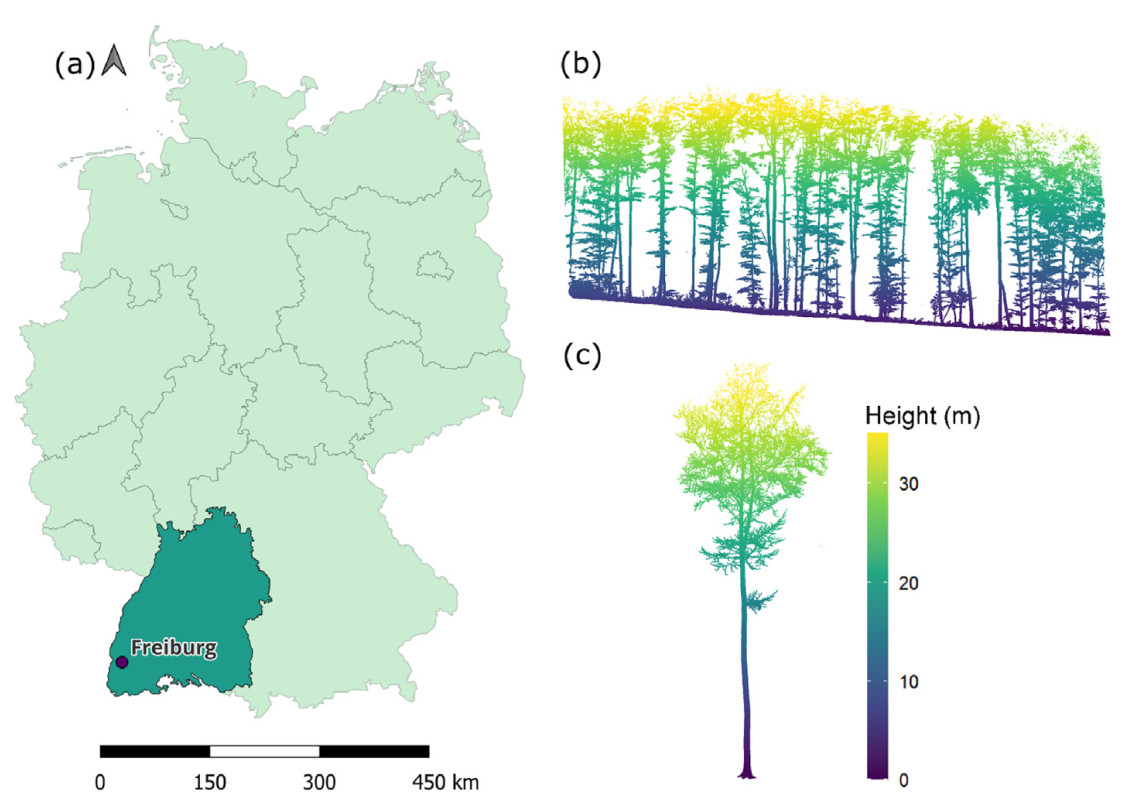
The study site is located in a forest research plot close to Freiburg (47°56′48.1″ N, 7°46′11.7″ E, 380 m a.s.l.) in Southwest Germany (Fig. 1). The forest stand is dominated by European beech (Fagus sylvatica), accounting for around 90% of the trees, which regenerated naturally and were managed using the target tree concept. The site is situated on a west-facing, moderately fresh calcareous scree slope and the soil is classified between a rendzina fusca and terra fusca. The climate at the study site can be described as humid temperate oceanic with warm summers (Köppen-Geiger: Cfb; Peel et al., 2007). In the climatic period from 1991 to 2020, the long-term annual average air temperature and annual precipitation sum amounted to 10.2 ℃ and 967 mm, respectively (DWD, 2023).
Figure
1.
Overview of the research site. (a) Map of Germany (light green area), Baden-Württemberg (dark blue area), and the research site close to Freiburg (purple point), source: BKG, 2023. (b) 3D point cloud cross-section of the studied forest site (colours indicate height above ground in m). (c) Example 3D point cloud of a tree. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)
The sample trees were randomly selected from the dominating and co-dominating beech trees (Kraft social classes 1–3; Kraft, 1884). After excluding unsuitable individuals, such as trees with crown damage or incompletely scanned trees, 67 sample trees remained. A summary of the general characteristics of the sample trees is presented in Table 1. With the substantial variation in crown lengths and crown widths, a wide range of crown types was encompassed.
Table
1.
Summary characteristics of the 67 sample beech trees: Age at breast height, tree height (h), diameter at breast height (dbh), crown length (cl), crown width (cw), and tree-ring width (trw).
TLS data was collected during winter dormancy in February 2020. A scanner of the type RIEGL VZ-400i (RIEGL Laser Measurement Systems GmbH, Horn, Austria) with a pulse repetition rate of 1200 kHz and a horizontal and vertical resolution of 0.04° was used. A multi-position scanning procedure was applied, meaning that scans were taken from multiple positions along a grid, ensuring full coverage of the forest stand.
The raw scan data was pre-processed using RiSCAN Pro software v.2.12.1 (RIEGL Laser Measurement Systems GmbH, Horn, Austria). This pre-processing step included co-registering, filtering, merging and down-sampling. From the registered point cloud of the stand each sample tree was segmented manually and remaining noise was removed cloud using CloudCompare software v2.12.beta (Girardeau-Montaut, 2022, see Fig. 1).
For each segmented tree point cloud, QSMs were computed using the TreeQSM-package v2.4.1 (Raumonen, 2022). To do this, first a set of hyperparameters was optimised for each tree using an automatic function provided by the package. Additionally, to better depict the thinner twigs commonly found in beech trees, the minimum cylinder diameter was set to 2 mm for all trees. As the model reconstruction process includes stochastic elements, 20 QSMs were computed for each tree using optimised parameters to ensure robust results. All subsequent data analyses were conducted using the statistical software environment R v4.2.1 (R Core Team, 2022).
2.3
Crown archetypes
The QSM output structure was imported to R with the help of the qsm2r package (Schindler, 2022). The information was used to compute a large set of crown variables, consisting of 14 morphology-related and 10 architecture-related variables. The variables were selected based on the literature review of the introduction chapter above with the aim to represent and model the functional relationship of crown morphology and branch architecture with resource acquisition, hydraulic conduction, and ultimately radial growth. Examples of the morphology variables are the crown width, length, volume, and crown fullness ratio and for the architectural variables branch dimensions, number of branching nodes, and water conduction path lengths. The full set of computed variables with explanations is presented in the supplementary material (Table S1).
The computed crown variables were averaged over all 20 QSMs of each tree. A principal component analysis (PCA) was conducted on the large set of variables to reduce collinearity by aggregating their information into non-correlated principal components. Thereby, we were able to reduce the number of variables to six principal components, which accounted for more than 90% of the variance in the initial set of crown variables. As part of addressing the first hypothesis, a k-means cluster analysis was used to categorise the sample trees into clusters based on their crown morphological and branch architectural characteristics in form of the PCA-reduced variable set. Hereby, observations were divided into clusters with observations in the same cluster having similar properties. Based on the within-cluster sum of squares we decided to categorise the sample trees into three clusters, which are referred to as crown archetypes in the following.
With the third hypothesis, we wanted to test whether specific crown characteristics influenced drought-affected tree radial growth. For this analysis step, we constrained our dataset using a subset of crown variables to avoid multicollinearity of predictor variables when formulating statistical models. Two branch architectural variables were selected, which possibly reflect the tree hydraulic structure. Their computation is described in the following paragraph.
The average length of the water conduction paths (cpl), i.e., the mean length from all branches, determined as the length from the branch tips to the stem base, was calculated by first identifying all terminal branches. Then, all branches in the related conduction path were selected and the branch lengths were summed up. An average length was calculated from all conduction path lengths of each tree. For the calculation of the average number of branching nodes per conduction path (nn), we identified all branching nodes by comparing the coordinates of all branch bases (starting points) against each other. To identify a branching node, i.e. a position where more than one branch originated from, three conditions had to be met by the compared branch bases. These conditions were, that (1) the branches had the same parent branch, (2) the distance between the branch bases was less than the diameter of the parent branch plus a buffer of two cm, and (3) the directional vector between the branch bases should not be similar to the directional vector of the parent branch (with a range of ±10%). The last condition served to avoid identifying two adjacent yet distinct nodes as a single one. The resulting information on the position of branching nodes was combined with the cylinder identities of each conduction path which were recorded while calculating the conduction path lengths. The number of nodes of all cylinders in the conduction path was summed up. An average number of branching nodes per conduction path was calculated by averaging over all conduction paths of the tree.
2.4
Tree-ring data
Increment cores were taken from all sample trees between the 30th of January and the 1st of February in 2023 using a standard increment borer (Haglöf Mora-Coretax, diameter 5.15 mm). Cores were taken perpendicular to the west-facing slope at breast height (1.3 m). The core samples were dried for two weeks and sanded sequentially using P120, P220 and P320 grit. Tree-ring widths (trws) were measured in a resolution of 0.01 mm using the PAST4 software package (Knibbe, 2004) combined with a high-precision linear table and a stereo microscope. All tree-ring width time series were cross-dated with a master chronology of another beech stand (approximately 100 km distant). An average chronology was created for all trees and for the three crown archetypes.
In addition to the absolute tree radial growth in form of the measured trws, the relative increment in basal area (riba) was calculated based on the common assumption of circular-shaped stems and the cumulative radius derived from annual radial increments.
riba=ibaba
(1)
Here, ba is the basal area calculated from the squared radius (sum of all trws) multiplied with pi and iba is the radial increment of ba during one year. Thus, riba can be considered as the basal area increment relative to the stem size.
As the TLS data only represents a momentary record of the crown morphology and architecture, the study period for further analyses was limited to the period from 2015 to 2022 to be cognisant of the fact that tree-ring growth would only correlate for some of the past years with the current tree architecture.
2.5
Environmental data
We calculated the Standardised Precipitation-Evapotranspiration Index (SPEI) for the assessment of drought stress severeness. The data for the computation was obtained from the Climate Data Center of the National German Weather Service (DWD, 2023). Monthly averaged air temperature and precipitation sums for the study site were extracted from a gridded dataset with a 1 km × 1 km raster using the R-package rdwd (Boessenkohl, 2022). We calculated the 12-month SPEI using the R-package SPEI (Beguería and Vicente-Serrano, 2023). We used an average of the SPEI12 between May and July for further analysis, as this three-month window showed the highest relevance for the measured tree-ring widths.
Additional to drought stress, we added further environmental variables regarding late frost and fructification. Late frost was specified as daily minimum temperatures below −3 ℃ around leaf burst and identified using gridded data (DWD, 2023). Notable fructification in Fagus sylvatica, an intrinsic effect influencing growth, was identified based on the annual reports of the forest condition survey in Southwest Germany that are based on multiple observations across Baden-Württemberg (see for example Meining et al., 2018).
2.6
Statistical analysis
To investigate the relationship between crown morphology, branch architecture and tree radial growth, we used linear mixed effects models (LMEMs) and the R-package lme4 (Bates et al., 2015). In all models, only one random effect was included, which was the randomly assigned tree identification number (Rtree). This was supposed to account for aspects that differ for every tree and which were not measured or accounted for otherwise (e.g., genotype, microclimate, and competition). All models were tested with both tree-ring width (trw) and relative basal area increment (riba) as response variable. Further, model diagnostic plots were generated to verify model assumptions, including model linearity, residual normality, residual homogeneity, and prediction quality.
To test the second part of the first hypothesis (H1), very simple models were built, estimating trw and riba (growth) based on the crown archetypes (archetype) (Eq. 2), where growth is either trw or riba, β0 and β1 are the model coefficients, Rtree is the random effect of the tree ID, and ε is the residual error.
growth=β0+β1×archetype+Rtree+ε
(2)
In order to determine the significance of the effects, a Welch-ANOVA was conducted. Additionally, estimated marginal means were computed for both models using the emmeans R-package (Lenth, 2023). Subsequently, pairwise comparisons between the crown archetypes were performed as post-hoc tests, with the p-values being adjusted using Tukey's correction procedure.
For the second hypothesis (H2), we checked whether the effect of drought on radial growth differed between the crown archetypes using the following model equation (Eq. 3), where growth is either trw or riba, β0 ‒ β3 are the model coefficients, archetype is the crown archetypes, SPEI12MJJ is the SPEI12 between May and July, Rtree is the random effect of the tree ID, and ε is the residual error.
In order to determine the significance of the effects, an ANOVA was conducted. As a post-hoc test, we tested for significant differences between the modelled slope coefficients of the archetypes using the emmeans R-package (Lenth, 2023).
With the third hypothesis (H3), we wanted to examine whether specific branch architectural variables had a significant impact on drought-affect radial growth. Therefore, we built a LMEM (Eq. 4), where growth is either trw or riba, β0 ‒ β8 are the model coefficients, Rtree is the random effect of the tree ID, and ε is the residual error. We added the dbh as a proxy for general productivity level, along with three environmental variables (SPEI12MJJ, frost, and fructification), because we expected them to explain a substantial portion of the variation in trw and riba. Both frost and fructification were added as dummy variables, indicating absence or presence of the respective event. In the model for riba, however, the dbh was not included, since riba inherently captures growth relative to the stem size. Furthermore, we incorporated an interaction term for SPEI12MJJ and fructification, because their effects on tree-radial growth were found to be interacting (Seifert and Müller-Starck, 2009; Hacket-Pain et al., 2017). Additionally, we incorporated the previously computed branch architectural variables cpl and nn plus their interaction as fixed effects to assess their effects on growth responses beyond the dbh and environmental factors. Before modelling, all continuous predictors were centred and scaled. Although the two crown variables exhibited high correlation (r > |0.7|), the VIF values were below 5 and multicollinearity only minimally affected variable estimates.
As the two branch architectural variables cpl and nn were closely correlated with crown length and crown size variables, respectively, we wanted to rule out the possibility that their effect could ultimately be traced back to crown dimensions after all. In order to do that, we fitted the same model with a three-way interaction between cpl, nn, and the crown volume.
3.
Results
3.1
Crown archetypes
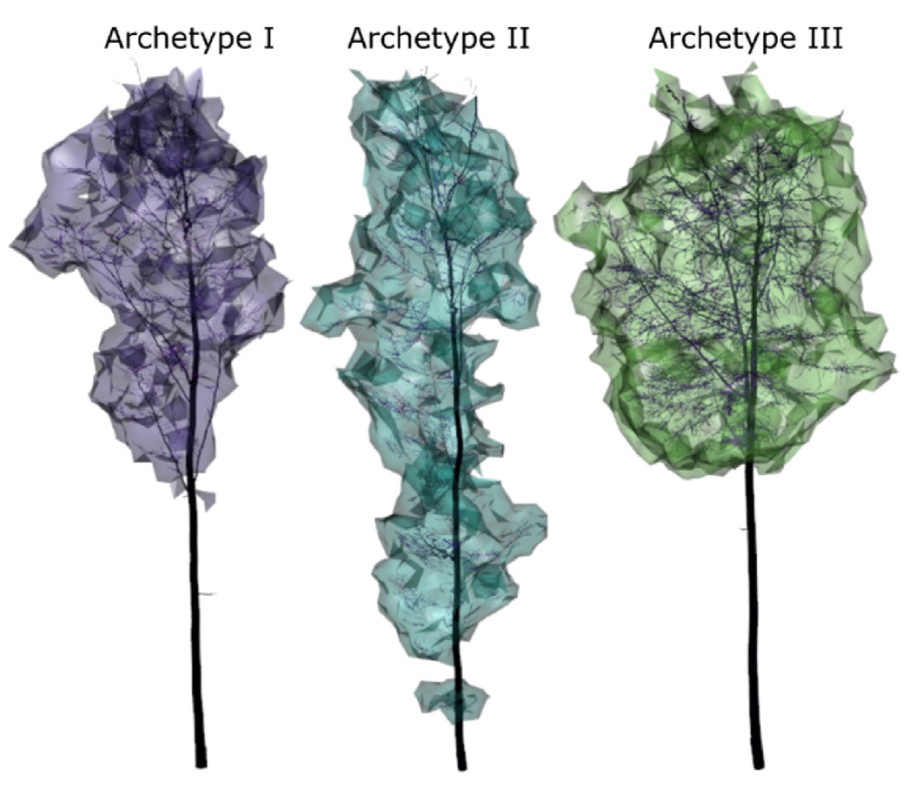
The sample trees were categorised into three archetypes based on their crown morphological and branch architectural characteristics (Table 2). The trees in Archetypes Ⅰ and Ⅱ had slimmer stems than the trees in Archetype Ⅲ, indicating a lower level of productivity. Additionally, the archetypes differed visibly in their crown form and size (Fig. 2). Crown volume increased from very small crowns in Archetype Ⅰ, to longer crowns in Archetype Ⅱ and wide, large crowns in Archetype Ⅲ. The long and slim crowns in Archetype Ⅱ are reflected in low values for the crown fullness ratio, which is the ratio between crown width and crown length. The top-heaviness, representing the height where the widest crown expansion occurs, was lowest for Archetype Ⅰ and highest for Archetype Ⅲ. The average length of the water conduction path was similar for trees in Archetypes Ⅰ and Ⅲ, but considerably lower for the trees with long crowns in Archetype Ⅱ. In contrast, the average number of branching nodes was lowest for Archetype Ⅰ and highest for Archetype Ⅱ. The latter also exhibited the smallest average length of branches, which was in turn largest for Archetype Ⅰ.
Table
2.
Overview on the characteristics of the crown archetypes. For each archetype, the average diameter at breast height (dbh) and averaged crown variables (crown volume (cv), crown fullness ratio (cfr), crown top-heaviness (cth), average length of conduction paths (cpl), and average number of nodes per conduction path (nn)) plus relating standard deviations are given.
Figure
2.
The three crown archetypes Ⅰ (purple), Ⅱ (blue) and Ⅲ (green). A representative sample tree is shown for each archetype in form of the related QSM illustrated in dark colours and the crown alpha shape in bright colours. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)
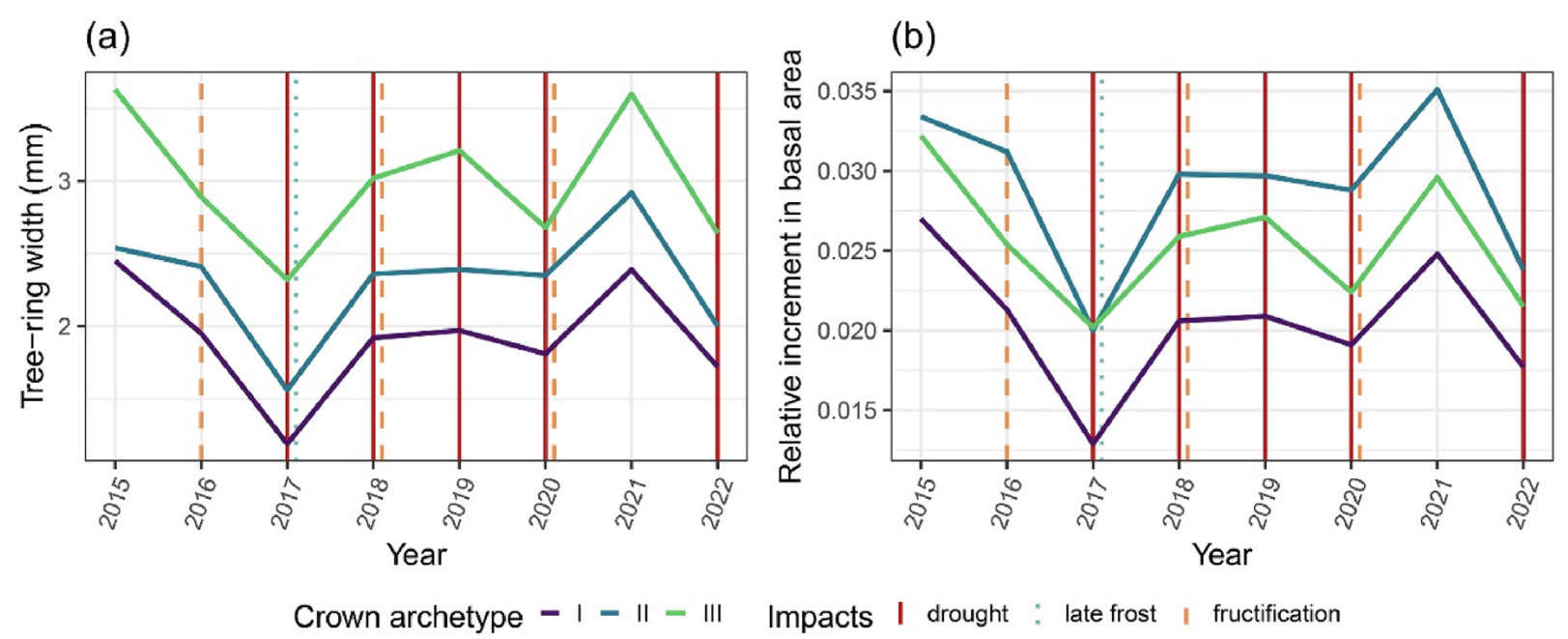
Monthly values of the SPEI12 are presented in Fig. 3. Except for the first half of 2015 and a slight recovery in 2021, the majority of the study period was characterised by ongoing drought. Measured trw and riba both averaged per crown archetype are illustrated in Fig. 4. Environmental impacts are represented as vertical lines. The level in trw differed between archetypes and increased in the order Ⅰ < Ⅱ < Ⅲ, while for relative basal area increment the order was Ⅰ < Ⅲ < Ⅱ. However, the temporal pattern of tree-ring widths was very similar for all archetypes, as lows and peaks occurred in the same years. The largest growth declines occurred in years with two combined environmental stresses or when drought stress followed a year with normal to wet conditions. Furthermore, the temporal pattern of riba closely resembled that of trw, which is why the following descriptions focus on variations in trw and only highlight differences to riba. Additional figures related to riba can be found in the supplementary material.
Figure
3.
Monthly values of the SPEI12 over the study period. Positive values (blue) indicate wet conditions and negative values (red) indicate dry conditions. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)
Figure
4.
Overview of annual tree growth patterns per crown archetype and environmental impacts between 2015 and 2022. Environmental impacts are highlighted as vertical lines, depicting drought events (where the average SPEI12MJJ was lower than −0.99, indicating moderate or severe drought), late frost events and fructification events. (a) Tree-ring widths in mm. (b) Relative increment in basal area.
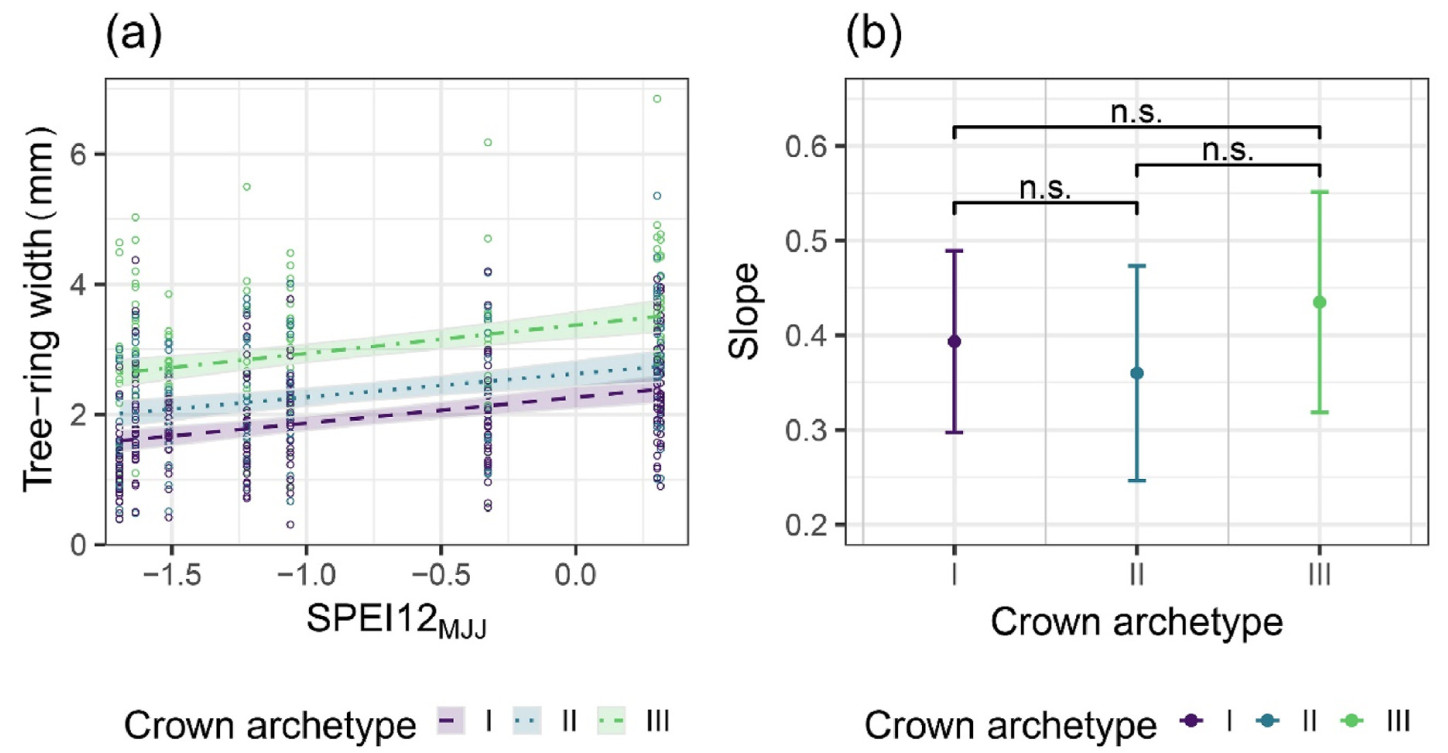
To test the effect of the categorisation of sample trees into the three crown archetypes on tree radial growth, we derived estimated marginal means from the models based on Eq. 2. Trees in Archetype Ⅲ formed significantly wider tree rings than the trees in the other two archetypes, for which trw was not significantly different (Fig. 5). Regarding riba, the only significant difference lay between archetypes Ⅰ and Ⅱ (Fig. S1), the latter exhibiting the highest estimate.
With a second set of models (Eq. 3), we examined whether drought effects on radial growth varied across crown archetypes (Fig. 6). Drought severeness was indicated as the drought index SPEI12 averaged over the months of May, June and July. As expected, trw increased with higher values of SPEI12MJJ, i.e., with wetter conditions. However, this effect did not differ between the crown archetypes for both trw and riba (Fig. 6 and Fig. S2).
Furthermore, we tested whether specific branch architectural variables had a significant effect on trw during ongoing drought conditions and whether they would hold information additional to the dbh and environmental factors. For this, the average length of water conduction paths (cpl) and the average number of branching nodes per conduction path (nn) were used in Eq. 4. According to the p-values, all model variables had significant effects except for cpl (see Table 3). As expected, the effects of dbh and SPEI12MJJ were positive and the effects of fructification and frost were negative. In addition, the effect of the SPEI12MJJ changed significantly in interaction with fructification events. The effects of the two branch architectural variables cpl and nn plus their interaction were positive, meaning that the positive effect of nn on trw is enhanced by higher cpl and vice versa (see Fig. S3). Further, the three-way interaction between cpl, nn, and crown volume was not significant. This confirms that nn and cpl explain variance in addition to the crown dimensions. Therefore, we were able to rule out the possibility that the significant effects of cpl and nn result from the underlying effects of crown dimension. As shown by the conditional R2, the model explains 71.0% of the variance, while 35.2% were explained by fixed effects (marginal R2) and 35.8% were explained by the individual tree ID which reflects tree-to-tree differences due to genetics, cambial age, local competition, site factors, or other non-considered factors (Cook, 1990). The R2 is in a typical range of an individual tree model for radial increment (Kunstler et al., 2011; Lundqvist et al., 2018). The diagnostic plots of the model verified the assumptions of model linearity and residual normality, as no significant deviations were visible (see Fig. S4). Also, the predicted values aligned well with the observed values. These results indicated an overall moderately good fit of the model, which identified several highly significant effects. The results on (Welch-)ANOVA and post-hoc-tests for the models based on Eqs. 2 and 3 can be found in the Supplementary Material.
Table
3.
Output of the complex model, estimating tree-ring widths based on the dbh, environmental impacts as well as branch architectural variables cpl and nn. All continuous predictors were scaled before modelling. Fructification and frost were entered as dummy variables, where the intercept represents the absence of the respective event.
In this study, we closely examined Fagus sylvatica crown characteristics by computing various crown morphological and branch architectural variables using TLS and QSMs. To our knowledge, we are the first to present crown archetypes for this species, which were developed based on the various crown variables and a cluster analysis. We combined the crown archetypes with measured tree-ring widths and showed that growth variations were properly described by the environmental impacts of drought, late frost and fructification. While the crown archetypes significantly differed in their general level of productivity, the effects of the environmental impacts did not generally differ between crown archetypes. However, certain branch architectural variables were decisive when predicting tree-ring widths, which indicates that some architectural types have a competitive edge regarding drought-affected growth against others.
4.1
Relationship between crown characteristics and radial growth
For the first time, crown archetypes were presented for European beech (Fig. 2 and Table 2). They can shortly be described as follows: small and short for Archetype Ⅰ, slim and long for Archetype Ⅱ, and wide and long for Archetype Ⅲ. Most branch architectural variables were correlated with crown size- or length-related variables. For example, the average number of nodes was positively correlated with crown size-related variables, and the average conduction path length was shorter for longer crowns. This is in accordance with Niklas (1994) who indicates that structural tree characteristics such as numbers and lengths of branches vary systematically with the stem diameter, which in turn is closely correlated with crown size-associated variables (Assmann, 1970). Therefore, we assume that a similar categorisation into crown archetypes might have been generated with a smaller set of mainly crown morphological variables.
Through resource sharing, tree crowns and radial growth are structurally and functionally linked (Shinozaki et al., 1964; Horn, 1971; Ross, 1981; Pretzsch, 2009). Thus, similar to the study of Pretzsch et al. (2022) on conifers, the identified crown archetypes for beech can be attributed to past competitive situations and current radial growth. Large-crowned trees with high photosynthetic capacities and potentially extensive rooting systems have access to substantial resources, including carbon, nutrients, and water (Niklas, 1992; Caldwell and Pearcy, 1994) and therefore exhibit wider tree-rings, indicating high productivity (Sundberg et al., 1993). Similarly, the radial growth differed significantly between the crown archetypes in our study, with large-crowned trees in crown Archetype Ⅲ forming the widest tree rings (Figs. 4 and 5). In contrast, slim tree crowns, such as in archetypes I and II, indicate highly competitive conditions and a lower resource acquisition resulting in lower radial growth (Dieler and Pretzsch, 2013). These results were not unexpected as the positive relationship between the tree crown size and radial growth is well-established (Fritts, 1976; Mäkelä and Valentine, 2006; Dieler and Pretzsch, 2013).
Figure
5.
Estimated marginal means of tree-ring widths in mm for the crown archetypes. The bars indicate the 95% confidence intervals. Different letters indicate a significant difference based on an alpha level of 5%.
Interestingly, in contrast to the absolute radial growth the relative increment in basal area was highest for the long-crowned trees in Archetype Ⅱ (Fig. S1). This might be due to the fact that the amount of resources (i.e., crown size) relative to the stem size (dbh) is highest for the trees with long and slim crowns. Therefore, trees with longer crowns have a higher resource availability than trees with shorter crowns at the same diameter, resulting in higher growth relative to the stem size, i.e., relative increment in basal area. We hypothesise that this finding might be limited to our special case of trees experiencing a long-lasting drought period, which might have favoured long-crowned trees because they can photosynthesise through less sun-exposed shade leaves, while sun-exposed leaves of wide-crowned individuals are forced to close down stomata due to drought conditions. This hypothesis is supported by the fact that the proportion of sun crown was smallest for Archetype Ⅱ trees. Overall, tree radial growth depends on tree and crown size, with absolute growth higher in trees with larger crowns and relative growth higher when the crown size relative to the stem is larger.
4.2
Relationship between crown characteristics, climatic factors, and radial growth
Further, we investigated the effects of the ongoing drought conditions on radial growth. Generally, drought conditions, as observed in previous studies (Pedersen, 1998; Chen et al., 2017; Chuste et al., 2019), have led to reduced radial growth of the sample trees. Moreover, we found that, compared to other three-month windows, the SPEI12 averaged over the months of May, June and July was most significant for estimating tree-ring widths. Accordingly, drought conditions during these months were found to be the most important factor for reducing tree radial growth (Mund et al., 2010; van der Maaten-Theunissen et al., 2013). A majority of the beech tree-ring is formed during this period (van der Maaten et al., 2012), regardless of an occurring drought (Kahle, 2006), rendering the water availability during these months a major influence on tree-ring growth of European beech. This was confirmed by the significant positive relationship of the SPEI12MJJ with the tree-ring width in this study (Fig. 6 and Table 3), reflecting reduced growth due to low water availability in the early summer months.
Figure
6.(a) Measured and estimated tree-ring widths in mm against the SPEI12MJJ values between 2015 and 2022 by crown archetype. The shaded areas represent 95% confidence intervals. (b) Modelled slope values per crown archetype with bars indicating the 95% confidence intervals and brackets indicating whether the difference between them is significant (s) or not (n.s.).
Interestingly, the identified principal effect of drought did not differ between crown archetypes, which, inter alia, represent the crown size (Figs. 4 and 6, Fig. S2). All archetypes reacted with reduced growth. Previous studies are not definite regarding the question of whether the climatic response of trees is mediated by crown type or size. Some studies show higher sensitivity in larger trees due to their higher resource and evapotranspirational demands (Condit et al., 1995; Bennett et al., 2015). Conversely, other studies find that smaller trees show a higher sensitivity to drought stress because of their limited water storage capacity and resource acquisition (Pichler and Oberhuber, 2007; De Luis et al., 2009). Additionally, some studies indicate no significant differences based on crown characteristics (Chhin et al., 2008; Campelo et al., 2013). In our study, we could not identify a superior crown archetype regarding drought-affected radial growth, as the effect of SPEI12MJJ on radial growth did not significantly differ between archetypes (Fig. 6 and Fig. S2).
Additionally, the late frost event in 2017 had an expected negative effect on the radial growth of the sample trees (Table 3). Previous research has shown similar results and highlights the sensitivity of beech cambial activity especially during leaf unfolding (Holmsgaard, 1962; Vitasse et al., 2019). The replacement of damaged foliage demands a high amount of resources which are then missing for radial growth (Dittmar et al., 2006; Stangler et al., 2017).
Further, we anticipated that two branch architectural variables would negatively impact drought-affected radial growth, as the water conductivity within a tree is determined by frictional resistance which increases with the number of branching nodes, conduction path length, and branch length (Hubbard et al., 2001; Rust and Roloff, 2002; Delzon et al., 2004). Consequently, longer paths and more nodes would lead to decreased photosynthetic capacities and ultimately carbon availability for radial growth. However, this was not confirmed by our results, as the effects of both variables and the interaction term were positive (Table 3). In other words, many nodes and long conduction paths resulted in higher radial growth and both effects reinforced each other (Table 3 and Fig. S3). This might suggest that expected hydraulic conduction-related effects are superposed by the effects of crown size. However, by tentatively adding a three-way interaction with crown volume to the model, we were able to rule out this possibility. The resulting insignificance of crown volume and the interaction suggests that even though the crown volume and the number of nodes per conduction path are highly correlated, the number of nodes and its interaction with the conduction path length explained a significant amount of variance in tree-ring widths additional to the crown size. Even though we are unable to explain this effect based on hydraulic conduction, it indicates that the drought-affected growth is not only influenced by the tree size (dbh) and environmental factors but also the branch architecture (Table 3). These results suggest, that, unlike our overall crown archetypes, trees belonging to certain architectural characteristics might have a competitive edge during drought conditions against others.
However, our results can only be seen as a first indication. It needs to be kept in mind, that we only studied one forest stand with one silvicultural treatment and a narrow age spectrum of sample trees and that these results might differ for other forest ecosystems. For different competition situations or tree species other crown characteristics might be more determinant for radial growth. Further, scan quality drastically decreases with increasing scanning distance resulting in significant under- and overestimations of branch dimensions (Morhart et al., 2024). Thus, the results of the present study need to be interpreted with great care, as they might be affected by these uncertainties.
4.3
Relationship between crown characteristics, fructification, and radial growth
In addition to climatic factors, fructification events are considerable stressors for trees due to enhanced resource consumption (Seifert and Müller-Starck, 2009; Meining et al., 2018). The negative effect of fructification on radial growth has been attributed to a carbon resource trade-off between reproductive and generative growth (Martín et al., 2015; Fathi and Tari, 2016; Hacket-Pain et al., 2017). While other authors do not agree (Mund et al., 2010), this assumption might still be true when carbon resources are depleted due to drought conditions (Hacket-Pain et al., 2017). Accordingly, we found that growth reductions were more pronounced when drought and fructification coincided (Table 3).
5.
Conclusions
In this study, we present an innovative approach to categorising the crowns of European beech trees into archetypes based on crown morphology and branch architecture and investigate their effects on radial growth. Trees with large crowns and large diameters demonstrated a higher growth level, which can be attributed to higher resource availability. Interestingly, trees with longer crowns and a larger shade crown proportion exhibited advantages regarding relative growth, as they seemed to capture more resources in proportion to their stem size. The crown archetypes exhibited comparable drought responses, resulting in the absence of any superior crown archetype in terms of radial growth under drought conditions. Yet, specific branch architectural characteristics were significant predictors for drought-affected tree radial growth: more branching nodes along water conduction paths and longer conduction paths were advantageous, indicating that trees with such characteristics have a competitive edge regarding radial growth under ongoing drought conditions.
These novel findings contribute to a deeper understanding of the structural and functional relationship between tree crowns and radial growth. If these results were confirmed by other studies, it would be possible to confidently identify superior crown characteristics for growth under drought conditions. This would enable foresters to promote specific crown types through thinning measures, thereby maintaining forest ecosystem stability under changing climate and related drought stress. Moreover, relating crown characteristics to underlying physiological processes might streamline the investigation of tree growth responses to climatic stressors. For instance, identifying potential connections between hydraulic conduction and the length of pathways could be beneficial for future research by reducing the need for in-depth examination of inner physiological processes. The presented methodology could be applied in future research, which should focus on validating and complementing our results across different sites, considering various thinning regimes and competition scenarios.
Funding and acknowledgements
We would like to acknowledge funding received from the Project “Hochaufgelöste Quantifizierung des Nährstoffentzuges bei verschiedenen Ernteszenarien der Buche” through the GFH Freiburg, which assisted with laser scanning. Dominik F. Stangler was supported by the German Federal Ministry of Food and Agriculture and the Federal Ministry for the Environment, Nature Conservation, Nuclear Safety and Consumer Protection (grant: 2219WK60C4). A special thanks goes also to the Municipality of Schallstadt, which provided the forest stand to our chair where we established the research plot. We thank for the support also by the district foresters Florian Faber and Jürgen Bucher. In addition, we would like to thank Dr. Christopher Morhart and Dr. Rafael Bohn Reckziegel for assistance with the Terrestrial Laser Scanning and our technician Robert Linne for assistance in the laboratory. We would further like to thank the editor John A. Kershaw for valuable comments that helped to substantially improve the manuscript.
Data availability
The datasets generated and/or analysed during the current study are available from the corresponding author on reasonable request.
Consent for publication
All authors gave their informed consent to this publication and its content.
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests:
Thomas Seifert reports financial support was provided by Gesellschaft zur Förderung der forst-und holzwirtschaftlichen Forschung an der Universität Freiburg im Breisgau e.V. Dominik Florian Stangler reports financial support was provided by the German Federal Ministry of Food and Agriculture and the German Federal Ministry for the Environment, Nature Conservation, Nuclear Safety and Consumer Protection. If there are other authors, they declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Ahmed, S., Pretzsch, H., 2023. TLidar-based crown shape indicates tree ring pattern in Norway spruce (Picea abies (L.) H. Karst) trees across competition gradients. A modeling and methodological approach. Ecol. Indic. 148, 110116. .
Archambeau, J., Ruiz-Benito, P., Ratcliffe, S., Fréjaville, T., Changenet, A., Muñoz Castañeda, J.M., Lehtonen, A., Dahlgren, J., Zavala, M.A., Benito Garzón, M., 2020. Similar patterns of background mortality across Europe are mostly driven by drought in European beech and a combination of drought and competition in Scots pine. Agric. For. Meteorol. 280, 107772. .
Assmann, E., 1970. The Principles of Forest Yield Study: Studies in the Organic Production, Structure, Increment and Yield of Forest Stands. Pergamon Press, Oxford.
Bates, D., Mächler, M., Bolker, B., Walker, S., 2015. Fitting linear mixed-effects models using lme4. J. Stat. Softw. 67 (1), 1–48. .
Bayer, D., Seifert, S., Pretzsch, H., 2013. Structural crown properties of Norway spruce (Picea abies [L.] Karst.) and European beech (Fagus sylvatica [L.]) in mixed versus pure stands revealed by terrestrial laser scanning. Trees 27 (4), 1035–1047. .
Bechtold, W.A., 2003. Crown-diameter prediction models for 87 species of stand-grown trees in the Eastern United States. South. J. Appl. For. 27 (4), 269–278.
Boessenkohl, B., 2022. Rdwd: select and download climate data from ’DWD’ (German weather Service). R package version 1.6.0. . (Accessed 7 December 2023).
Bennett, A.C., McDowell, N.G., Allen, C.D., Anderson-Teixeira, K.J., 2015. Larger trees suffer most during drought in forests worldwide. Nat. Plants 1 (10), 1–5. .
Bigler, C., Vitasse, Y., 2021. Premature leaf discoloration of European deciduous trees is caused by drought and heat in late spring and cold spells in early fall. Agric. For. Meteorol. 307, 108492. .
BKG, 2023. Open data of german federal agency for cartography and geodesy. . (Accessed 23 November 2023).
Boessenkohl, B., 2022. Rdwd: select and download climate data from ’DWD’ (German weather Service). R package version 1.6.0. . (Accessed 7 December 2023).
Cailleret, M., Jansen, S., Robert, E.M.R., Desoto, L., Aakala, T., Antos, J.A., Beikircher, B., Bigler, C., Bugmann, H., Caccianiga, M., Čada, V., Camarero, J.J., Cherubini, P., Cochard, H., Coyea, M.R., Čufar, K., Das, A.J., Davi, H., Delzon, S., Dorman, M., Gea-Izquierdo, G., Gillner, S., Haavik, L.J., Hartmann, H., Heres, A., Hultine, K.R., Janda, P., Kane, J.M., Kharuk, V.I., Kitzberger, T., Klein, T., Kramer, K., Lens, F., Levanic, T., Calderon, J.C.L., Lloret, F., Lobo-Do-Vale, R., Lombardi, F., Rodriguez, R.L., Makinen, H., Mayr, S., Meszaros, I., Metsaranta, J.M., Minunno, F., Oberhuber, W., Papadopoulos, A., Peltoniemi, M., Petritan, A.M., Rohner, B., Sanguesa-Barreda, G., Sarris, D., Smith, J.M., Stan, A.B., Sterck, F., Stojanovic, D.B., Suarez, M.L., Svoboda, M., Tognetti, R., Torres-Ruiz, J.M., Trotsiuk, V., Villalba, R., Vodde, F., Westwood, A.R., Wyckoff, P.H., Zafirov, N., Martínez-Vilalta, J., 2017. A synthesis of radial growth patterns preceding tree mortality. Glob. Change Biol. 23 (4), 1675–1690. .
Caldwell, M.M., Pearcy, R.W., 1994. Exploitation of Environmental Heterogeneity by Plants: Ecophysiological Processes above- and Belowground. Academic Press. .
Campelo, F., Vieira, J., Nabais, C., 2013. Tree-ring growth and intra-annual density fluctuations of Pinus pinaster responses to climate: does size matter? Trees (Berl.) 27 (3), 763–772. .
Canham, C.D., 1988. Growth and canopy architecture of shade-tolerant trees: response to canopy gaps. Ecology 69 (3), 786–795. .
Chen, L., Huang, J.-G., Alam, S.A., Zhai, L., Dawson, A., Stadt, K.J., Comeau, P.G., 2017. Drought causes reduced growth of trembling aspen in western Canada. Glob. Change Biol. 23 (7), 2887–2902. .
Chhin, S., Hogg, E.H. (Ted), Lieffers, V.J., Huang, S., 2008. Potential effects of climate change on the growth of lodgepole pine across diameter size classes and ecological regions. For. Ecol. Manag. 256 (10), 1692–1703. .
Chuste, P.-A., Massonnet, C., Gérant, D., Zeller, B., Levillain, J., Hossann, C., Angeli, N., Wortemann, R., Bréda, N., Maillard, P., 2019. Short-term nitrogen dynamics are impacted by defoliation and drought in Fagus sylvatica L. branches. Tree Physiol. 39 (5), 792–804. .
Condit, R., Hubbell, S.P., Foster, R.B., 1995. Mortality rates of 205 neotropical tree and shrub species and the impact of a severe drought. Ecol. Monogr. 65 (4), 419–439. .
Cook, E.R., 1990. Methods of dendrochronology. Applications in the Environmental Sciences. Springer, Dordrecht. .
De Luis, M., Novak, K., Čufar, K., Raventós, J., 2009. Size mediated climate–growth relationships in Pinus halepensis and Pinus pinea. Trees 23 (5), 1065–1073. .
Delzon, S., Sartore, M., Burlett, R., Dewar, R., Loustau, D., 2004. Hydraulic responses to height growth in maritime pine trees. Plant Cell Environ. 27 (9), 1077–1087. .
Dieler, J., Pretzsch, H., 2013. Morphological plasticity of European beech (Fagus sylvatica L.) in pure and mixed-species stands. For. Ecol. Manag. 295, 97–108. .
Disney, M.I., Boni Vicari, M., Burt, A., Calders, K., Lewis, S.L., Raumonen, P., Wilkes, P., 2018. Weighing trees with lasers: advances, challenges and opportunities. Interface Focus. 8 (2), 20170048. .
Dittmar, C., Fricke, W., Elling, W., 2006. Impact of late frost events on radial growth of common beech (Fagus sylvatica L.) in Southern Germany. Eur. J. For. Res. 125 (3), 249–259. .
DWD, 2023. Climate Data Center: free access to many climate data of the DWD. . (Accessed 7 December 2023).
Fathi, A., Tari, D.B., 2016. Effect of drought stress and its mechanism in plants. Int. J. Life Sci. 10 (1), 1–6. .
Fritts, H., 1976. Tree Rings and Climate. Academic Press. .
Fruh, T., 1995. Entwicklung eines Simulationsmodells zur Untersuchung des Wasserflusses in der verzweigten Baumarchitektur. Forschungszentrum Waldökosysteme, Göottingen.
Früh, T., Kurth, W., 1999. The hydraulic system of trees: theoretical framework and numerical simulation. J. Theor. Biol. 201 (4), 251–270. .
Girardeau-Montaut, D., 2022. CloudCompare: a 3D point cloud and mesh processing software, Version 2.12 beta. . (Accessed 7 December 2023).
Givnish, T.J., 1988. Adaptation to sun and shade: a whole-plant perspective. Funct. Plant Biol. 15 (2), 63–92. .
Hacket-Pain, A.J., Lageard, J.G.A., Thomas, P.A., 2017. Drought and reproductive effort interact to control growth of a temperate broadleaved tree species (Fagus sylvatica). Tree Physiol. 37 (6), 744–754. .
Holmsgaard, E., 1962. Influence of weather on growth and reproduction of beech. Metsantutkimuslaitoksen Julk. 55, 5.
Horn, H.S., 1971. The Adaptive Geometry of Trees. Princeton University Press, USA.
Hubbard, R.M., Ryan, M.G., Stiller, V., Sperry, J.S., 2001. Stomatal conductance and photosynthesis vary linearly with plant hydraulic conductance in ponderosa pine. Plant Cell Environ. 24 (1), 113–121. .
Hutchings, M.J., de Kroon, H., 1994. Foraging in plants: the role of morphological plasticity in resource acquisition. In: Begon, M., Fitter, A.H. (Eds.), Advances in Ecological Research, vol. 25. Academic Press, pp. 159–238. .
Hutchison, B.A., Matt, D.R., 1977. The distribution of solar radiation within a deciduous forest. Ecol. Monogr. 47 (2), 185–207. .
IPCC, 2022. Climate Change 2022: Impacts, Adaptation and Vulnerability. Cambridge University Press. .
Jucker, T., Bouriaud, O., Coomes, D., 2015. Crown plasticity enables trees to optimize canopy packing in mixed-species forests. Funct. Ecol. 29, 1078–1086. .
Kahle, H.-P., 2006. Impact of the drought in 2003 on intra- and inter-annual stem radial growth of beech and spruce along an altitudinal gradient in the Black Forest, Germany. TRACE-Tree Rings Archaeol. Climatol. Ecol. 151–163.
Knibbe, B., 2004. PAST4 Q19: Personal Analysis System for Tree Ring Research – Instruction Manual. SCIEM, Vienna, Version 4.
Kozlowski, T.T., Pallardy, S.G., 1997. Growth Control in Woody Plants. Academic Press. .
Kraft, G., 1884. Beiträge zur Lehre von den Durchforstungen, Schlagstellungen und Lichtungshieben. Klindworth’s Verlag, Hamburg.
Kunstler, G., Albert, C., Courbaud, B., Lavergne, S., Thuiller, W., Vieilledent, G., Zimmermann, N., Coomes, D., 2011. Effects of competition on tree radial-growth vary in importance but not in intensity along climatic gradients. J. Ecol. 99, 300–312. .
Larysch, E., Stangler, D.F., Nazari, M., Seifert, T., Kahle, H.-P., 2021. Xylem phenology and growth response of European beech, silver fir and Scots pine along an elevational gradient during the extreme drought year 2018. Forests 12 (1), 1. .
Lebourgeois, F., Drénou, C., Bouvier, M., Lemaire, J., 2015. Characterisation of decaying atlantic pedunculate oak stands - effects of drought and relations with crown architecture. Rev. For. Fr. 67 (4), 333–351.
Lenth, R.V., 2023. Emmeans: estimated marginal means, aka least-squares means. R package version 1.8.5. . (Accessed 7 December 2023).
Leuschner, C., Ellenberg, H., 2017. Ecology of central European non-forest vegetation: coastal to alpine, natural to man-made habitats. Vegetation Ecology of Central Europe, Volume Ⅱ. Springer, Cham. .
Lundqvist, S.-O., Seifert, S., Grahn, T., Olsson, L., García-Gil, M.R., Karlsson, B., Seifert, T., 2018. Age and weather effects on between and within ring variations of number, width and coarseness of tracheids and radial growth of young Norway spruce. Eur. J. For. Res. 137 (5), 719–743. .
Mäkelä, A., Valentine, H.T., 2006. Crown ratio influences allometric scaling in trees. Ecology 87 (12), 2967–2972. .
Martín, D., Vázquez-Piqué, J., Carevic, F.S., Fernández, M., Alejano, R., 2015. Trade-off between stem growth and acorn production in holm oak. Trees 29 (3), 825–834. .
McDowell, N.G., Fisher, R.A., Xu, C., Domec, J.C., Hölttä, T., Mackay, D.S., Sperry, J.S., Boutz, A., Dickman, L., Gehres, N., Limousin, J.M., Macalady, A., Martínez-Vilalta, J., Mencuccini, M., Plaut, J.A., Ogée, J., Pangle, R.E., Rasse, D.P., Ryan, M.G., Sevanto, S., Waring, R.H., Williams, A.P., Yepez, E.A., Pockman, W.T., 2013. Evaluating theories of drought-induced vegetation mortality using a multimodel–experiment framework. New Phytol. 200 (2), 304–321. .
Meining, S., Puhlmann, H., Hartmann, P., Hoch, R., 2018. Waldzustandsbericht 2018. Forstliche Versuchs- und Forschungsanstalt Baden-Württemberg. . (Accessed 7 December 2023).
Morhart, C., Schindler, Z., Frey, J., Sheppard, J.P., Calders, K., Disney, M., Morsdorf, F., Raumonen, P., Seifert, T., 2024. Limitations of estimating branch volume from terrestrial laser scanning. Eur. J. For. Res. .
Mund, M., Kutsch, W.L., Wirth, C., Kahl, T., Knohl, A., Skomarkova, M.V., Schulze, E.-D., 2010. The influence of climate and fructification on the inter-annual variability of stem growth and net primary productivity in an old-growth, mixed beech forest. Tree Physiol. 30 (6), 689–704. .
Muth, C.C., Bazzaz, F.A., 2003. Tree canopy displacement and neighborhood interactions. Can. J. For. Res. 33 (7), 1323–1330. .
Niklas, K.J., 1992. Plant Biomechanics: an Engineering Approach to Plant Form and Function. University of Chicago Press, Chicago.
Niklas, K.J., 1994. Plant Allometry: the Scaling of Form and Process. University of Chicago Press, Chicago.
Obladen, N., Dechering, P., Skiadaresis, G., Tegel, W., Kessler, J., Hollerl, S., Kaps, S., Hertel, M., Dulamsuren, C., Seifert, T., 2021. Tree mortality of European beech and Norway spruce induced by 2018-2019 hot droughts in central Germany. Agric. For. Meteorol. 307, 108482. .
Pedersen, B.S., 1998. The role of stress in the mortality of midwestern oaks as indicated by growth prior to death. Ecology 79 (1), 79–93. .
Peel, M.C., Finlayson, B.L., McMahon, T.A., 2007. Updated world map of the Köppen-Geiger climate classification. J. Hydrol. Earth Syst. Sci. 11 (5), 1633–1644. .
Pichler, P., Oberhuber, W., 2007. Radial growth response of coniferous forest trees in an inner Alpine environment to heat-wave in 2003. For. Ecol. Manag. 242 (2), 688–699. .
Pretzsch, H., 2009. Forest dynamics, growth, and yield: a review, analysis of the present state, and perspective. In: Pretzsch, H. (Ed.), Forest Dynamics, Growth and Yield: from Measurement to Model. Springer. .
Pretzsch, H., 2021. Tree growth as affected by stem and crown structure. Trees (Berl.) 35 (3), 947–960. .
Pretzsch, H., Ahmed, S., Jacobs, M., Schmied, G., Hilmers, T., 2022. Linking crown structure with tree ring pattern: methodological considerations and proof of concept. Trees (Berl.) 36 (4), 1349–1367. .
Pretzsch, H., Schutze, G., 2005. Crown allometry and growing space efficiency of Norway Spruce (Picea abies [L.] Karst.) and European Beech (Fagus sylvatica L.) in pure and mixed stands. Plant Biol. 7, 628-639. .
R Core Team, 2022. R: a language and environment for statistical computing. . (Accessed 7 December 2023).
Raumonen, P., 2022. TreeQSM: reconstruction of quantitative structure models for trees from point cloud data version 2.4.1. . (Accessed 7 December 2023).
Roloff, A., 2001. Baumkronen. Verständnis und praktische Bedeutung eines komplexen Naturphänomens. Verlag Eugen Ulmer GmbH & Co, Stuttgart.
Ross, J., 1981. The Radiation Regime and Architecture of Plant Stands. Springer, Dordrecht. .
Rust, S., Roloff, A., 2002. Reduced photosynthesis in old oak (Quercus robur): the impact of crown and hydraulic architecture. Tree Physiol. 22 (8), 597–601. .
Schindler, Z., 2022. qsm2r: import and analyze QSMs from TreeQSM in R. . (Accessed 7 December 2023).
Seifert, T., Müller-Starck, G., 2009. Impacts of fructification on biomass production and correlated genetic effects in Norway spruce (Picea abies [L.] Karst.). Eur. J. For. Res. 128 (2), 155–169. .
Shinozaki, K., Yoda, K., Hozumi, K., Kira, T., 1964. A quantitative analysis of plant form – the pipe model theory: Ⅰ. Basic analyses. Jpn. J. Ecol. 14, 97–105.
Stangler, D.F., Hamann, A., Kahle, H.-P., Spiecker, H., Mäkelä, A., 2017. A heat wave during leaf expansion severely reduces productivity and modifies seasonal growth patterns in a northern hardwood forest. Tree Physiol. 37 (1), 47–59. .
Sundberg, B., Ericsson, A., Little, C.H.A., Näsholm, T., Gref, R., 1993. The relationship between crown size and ring width in Pinus sylvestris L. stems: dependence on indole-3-acetic acid, carbohydrates and nitrogen in the cambial region. Tree Physiol. 12 (4), 347–362. .
Tilman, D., 1988. Plant Strategies and the Dynamics and Structure of Plant Communities. Princeton University Press, Princeton.
Valladares, F., Gianoli, E., Gomez, J.M., 2007. Ecological limits to plant phenotypic plasticity. New Phytol. 176 (4), 749–763. .
Maaten, E. van der, Maaten-Theunissen, M. van der, Spiecker, H., 2012. Temporally resolved intra-annual wood density variations in European beech (Fagus sylvatica L.) as affected by climate and aspect. Ann. For. Res. 113–124. .
van der Maaten-Theunissen, M., Kahle, H.-P., van der Maaten, E., 2013. Drought sensitivity of Norway spruce is higher than that of silver fir along an altitudinal gradient in southwestern Germany. Ann. For. Sci. 70 (2), 185–193. .
Vitasse, Y., Bottero, A., Cailleret, M., Bigler, C., Fonti, P., Gessler, A., Lévesque, M., Rohner, B., Weber, P., Rigling, A., Wohlgemuth, T., 2019. Contrasting resistance and resilience to extreme drought and late spring frost in five major European tree species. Glob. Change Biol. 25 (11), 3781–3792. .
Wang, Y.P., Jarvis, P.G., 1990. Influence of crown structural properties on PAR absorption, photosynthesis, and transpiration in Sitka spruce: application of a model (MAESTRO). Tree Physiol. 7 (1-2-3-4), 297–316. .
Table
1.
Summary characteristics of the 67 sample beech trees: Age at breast height, tree height (h), diameter at breast height (dbh), crown length (cl), crown width (cw), and tree-ring width (trw).
Table
2.
Overview on the characteristics of the crown archetypes. For each archetype, the average diameter at breast height (dbh) and averaged crown variables (crown volume (cv), crown fullness ratio (cfr), crown top-heaviness (cth), average length of conduction paths (cpl), and average number of nodes per conduction path (nn)) plus relating standard deviations are given.
Table
3.
Output of the complex model, estimating tree-ring widths based on the dbh, environmental impacts as well as branch architectural variables cpl and nn. All continuous predictors were scaled before modelling. Fructification and frost were entered as dummy variables, where the intercept represents the absence of the respective event.
DownLoad:
Email Alerts
RSS Feeds