| Citation: | Asadilla Yusup, Ümüt Halik, Maierdang Keyimu, Tayierjiang Aishan, Abdulla Abliz, Babierjiang Dilixiati, Jianxin Wei. Trunk volume estimation of irregular shaped Populus euphratica riparian forest using TLS point cloud data and multivariate prediction models[J]. Forest Ecosystems, 2023, 10(1): 100082. DOI: 10.1016/j.fecs.2022.100082 |
| Abbreviations | |
| LiDAR | Light detection and ranging |
| TLS | Terrestrial laser scanning |
| RI | Reflection intensity |
| Vt | Trunk volume |
| H | Tree height |
| TH | Trunk height |
| BH | Under branch height |
| DBH | Diameter at breast height |
| CD | Crown diameter |
| CA | Crown area |
| BD | Basal trunk diameter |
| Di | Diameter of the trunk at the different heights |
| RMSE | Root mean square error |
| BIC | Bayesian information criterion |
| ME | Mean prediction error |
| MAE | Mean absolute error |
| EF | Modeling efficiency |
Measuring tree volume and establishing prediction models are essential tasks for the precise determination of forest resources and sustainable management (Pretzsch, 2009; Martí et al., 2012; Sun et al., 2016; Avitabile and Camia, 2018; Yang et al., 2022). Trunk volume (Vt) accounts for the largest proportion (60%–70%) of total tree volume (West, 2004; Wang and Lu, 2012; Li et al., 2020). An accurate calculation of Vt is needed to estimate stand volume (Bienert et al., 2014), which can be converted into dry weight using the wood density factor and further predict the forest total biomass and carbon storage with the smallest bias (Lehtonen et al., 2004; Yu et al., 2013; Sagang et al., 2018; Demol et al., 2022).
Vt measurement methods include direct measurement of felled trees and indirect measurement of standing trees (Feng et al., 2005; Parresol and Thomas, 2011). Previous studies required labor intensive, time-consuming, and seriously destructive fieldwork that included harvesting trees and measuring diameters along the trunk to obtain Vt (López-Martínez et al., 2019; Zuleta et al., 2022). The difficulty of direct determination of volume using section calculations makes it advisable to define allometric relationships based on unbiased samples and accurate measurements (Moscovich and Brena, 2006). Leão et al. (2021) found that a minimum of 80 sample trees was required to fit accurate tree volume allometric estimation models for the Amazon rainforest. In the determination of standing tree volume, the trunk is generally regarded a regular cylindrical geometrical shape, and the volume can be indirectly calculated using empirical methods applied to the tree height (H) and diameter at breast height (DBH) (Martí et al., 2012; Wang et al., 2016). Inoue et al. (2012) constructed single and double input volume models using H and DBH for bamboo species to estimate the amount of bamboo resources in Japan. However, in some forests, tree trunk shapes are affected by factors such as tree species, age, site conditions, and management measures, which influence the relationship between DBH and H, as well as the tree volume. These create limitations in applying this regular growth model (Feldpausch et al., 2011; Hunter et al., 2013; Sande et al., 2017). Tortuosity and irregularity of the trunks from the base to the canopy make it difficult to collect data and estimate volume and biomass. Using simple elementary equations to reflect the complete volume of a tree trunk is difficult (Bettinger et al., 2009). Silva et al. (2019) found a low correlation of H and DBH with the volume of Brazilian Savanna trees due to the tortuosity of the bole; mixed regression model analyses using artificial intelligent techniques demonstrated that this method has great potential to estimate the volume of individual trees. Therefore, developing tree volumetric models for each site results in an extensive sampling effort, owing to the variability in dendrometric data in the forest area (Akindele and Lemay, 2006; Leão et al., 2021).
Euphrates poplar (Populus euphratica Oliv.) is the dominant tree species in desert riparian forest ecosystems in arid regions. It has a very wide natural distribution range, occurring from North Africa across Middle East and Central Asia to western China (Monda et al., 2008; Thomas and Lang, 2020). These riparian forests provide essential ecosystem services such as maintenance of ecological stability, increased watershed protection, prevention of sandstorms, and reduction of soil erosion and desertification (Chen et al., 2013; Betz et al., 2015; Halik et al., 2019; Keram et al., 2019, 2021). Approximately 54% of the P. euphratica worldwide is distributed along the seasonally flooded Tarim River in NW China, which is one of the largest inland rivers in the world (Ling et al., 2015). In recent decades, these desert poplar forests have degraded and even disappeared because of reduced water flow and flooding frequency as well as increased soil salinization (Thevs et al., 2012; Aishan et al., 2015, 2016). In 2000, the Chinese government implemented a manmade ecological water conveyance project to protect riparian forests in the lower reaches of the Tarim River (Xu et al., 2007). Interest in measuring forest structural attributes such as stand volume, biomass, and carbon stock has increased in order to evaluate the ecological effect of restoration projects, which have received extensive investment (Keyimu et al., 2017a; Ling et al., 2020). However, the growth and development conditions of P. euphratica differ along riverside–desert gradients by the Tarim River (Thomas and Lang, 2020; Han and He, 2020), which challenges the development of a general tree volume prediction model. Advanced detection techniques such as light detection and ranging (LiDAR) active remote sensing technology may help to nondestructively and accurately obtain the volume of irregularly shaped P. euphratica trees.
As one of the LiDAR platforms, terrestrial laser scanning (TLS) has been extensively applied in forest inventories for detailed data collection to estimate various variables such as forest structural attributes, leaf area index, wood quality, and biomass (Leeuwen and Nieuwenhuis, 2010; Guo et al., 2018; Liu et al., 2022) while minimizing laborious fieldwork, thereby maximizing the number of sampled trees (Vicari et al., 2019; Calders et al., 2020; Bauwens et al., 2021). Its dense three-dimensional (3D) point cloud data allows characterization of an individual tree at a millimetric level of detail, enabling researchers to acquire tree parameters (Hackenberg et al., 2015). TLS data collection and processing for optimal setup require only one-sixth of the time necessary to obtain a field reference (Saarinen et al., 2017).
In addition to the 3D structure, TLS measures the strength of the reflected light back to the sensor, which is commonly referred to as reflection intensity (RI). The laser RI is mainly influenced by the reflectance of the object (Song et al., 2002). The surface laser reflectance determines the intensity value, which is a function of surface texture and roughness (Arianna and Teza, 2008; Junttila et al., 2021). RI has been shown to be useful for tree species classification (Donoghue et al., 2007), planimetric offset correction (Vosselman, 2012), and aboveground biomass prediction (García et al., 2010). Lu et al. (2014) developed a method to segment individual trees based on the RI of LiDAR data. Reitberger et al. (2009) pointed out that RI has the potential to detect stem points via analysis of LiDAR waveform.
In the present study, we applied TLS point cloud RI information to acquire the Vt of P. euphratica and construct a prediction model for Vt and tree structural parameters. The main objectives were to (1) extract 3D information on irregularly shaped tree trunks of P. euphratica using the TLS intensity value; (2) measure trunk structural parameters in order to calculate the Vt of the trees and verify its accuracy; and (3) construct multiple Vt prediction models with the best performance.
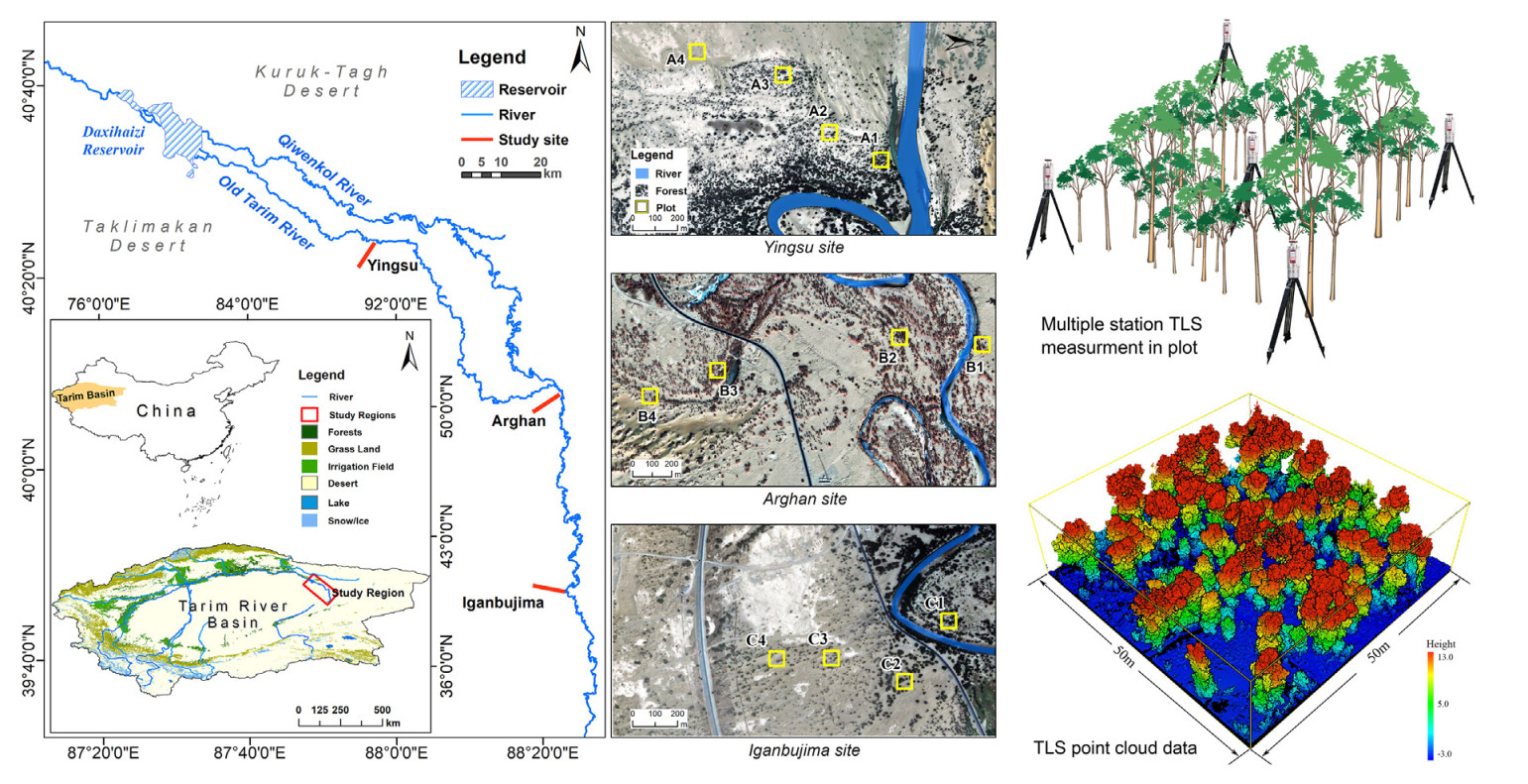
The field work was conducted in the lower reaches of the Tarim River, between the Taklimakan and Kuruk–Tagh deserts in northwest China (Fig. 1). This area has extremely arid desert climatic conditions (Kottek et al., 2006), with an annual precipitation of 20–50 mm and potential evaporation of 2, 429–2, 910 mm per year. High temperatures in July can reach 45 ℃, the lowest temperature in January can reach −30 ℃, the average annual temperature is about 10 ℃, and mean annual sunshine hours are about 2, 900 h, making this area one of the most extreme arid regions in the world (Thomas et al., 2016). According to the Food and Agriculture Organization classification, soil types in the study area include Fluvisols, Gleysols, Solonchak, and Arenosols (Thevs et al., 2012). The local groundwater system is recharged from the Tarim River water via bank infiltration (Halik et al., 2019). Desert riparian forests are found along river floodplains (Keyimu et al., 2017b). The dominant tree species is P. euphratica, the main shrubs are Tamarix ramosissima, Tamarix hispida, Lycium ruthenicum, and the main herbaceous plants are Phragmites australis, Hexinia polydichotoma, Alhagi sparsifolia, Karelinia caspia, Apocynum venetum, and Glycyrrhiza inflata (Kurban et al., 2019; Yusup et al., 2022).
Field data were collected in May 2020 at three sites at the lower reaches of the Tarim River, namely the Yingsu, Arghan, and Iganbujima (Fig. 1). A total of 12 square plots (A1–A4, B1–B4, and C1–C4) of side lengths 50 m were established at 20, 200, 400, and 600 m from the river channel at each site, and P. euphratica was the monospecific tree in all plots. To capture whole 3D information at each plot, we used Riegl VZ-1000 TLS (Riegl, Co. Ltd. Horn, Austria) equipment arranged at five positions (located in the center and periphery of the four corner positions of the plot) in each plot (Fig. 1). The scanning range of the TLS device was set to a vertical angle of 30°–130°, a horizontal angle of 0°–360°, and a scanning distance of 450 m, in fine scanning mode. The Riegl VZ-1000 employs a 1, 550-nm laser with onboard waveform processing that allows it to record multiple returns for each laser pulse, and the laser pulse repetition rate was 300 kHz. We recorded multiple returns for each laser pulse; scanning accuracy was 5 mm per 100 m; laser emission frequency was 30, 000 points·s−1, and time spent was 12 min per site. The measurement process was carried out under a wind speed of less than 3 m·s−1 with no precipitation (Yusup et al., 2020).
The TLS was set up with multiple scan positions in each plot, and the trees were scanned from five different directions. The original TLS data contained the spatial coordinates (x, y, z) and RI information for each point cloud. Riscan Pro (V.2.7, Riegl, Co. Ltd. Horn, Austria) was used to perform coordinate co-registration to multi-station TLS data, which were merged into one set of 3D data with a standard deviation < 0.05 m. Then, point clouds were exported to Las1.2 format for further processing. The LiDAR360 (V. 4.0, Green Valley, Co. Ltd. Beijing, China) was used to perform denoising and classifying the ground and aboveground point clouds according to the lowest elevation value at each point. Ground points were normalized to eliminate the terrain influence on tree height acquisition (Guo et al., 2018). The aboveground points were then manually classified as trees or shrubs. The TLS data processing flowchart is shown in Fig. 2.
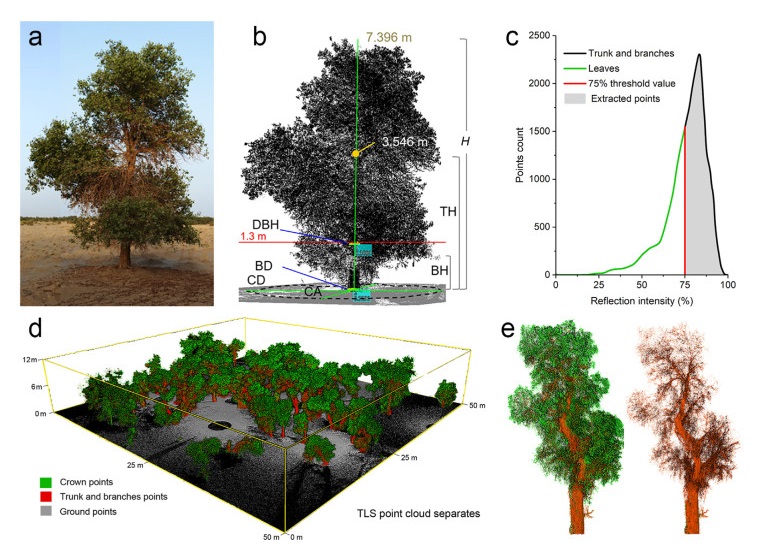
The point clouds at 1.25–1.35 m height interval was extracted from the elevation-normalized data and interpolated into a raster image at a resolution of 1 cm, and the points were fitted to a circle using the two-dimensional Hough transforms method (Guo et al., 2018) for batch extraction of the DBH value. Based on each DBH location, the individual tree seed points were generated. The trees were segmented according to the seed point's positions to obtain the H, crown diameter (CD), and crown area (CA) parameters. A total number of 803 trees were segmented by TLS data, and the structural attributes of each tree were acquired; the average values of parameters are shown in Table 1.
| Section | Plots | Area (m2) | Distance from the river (m) | Altitude (m) | Tree density (trees·ha−1) | Sampled trees | Mean values of tree structural attributes | |||
| H (m) | DBH (m) | CD (m) | CA (m2) | |||||||
| Yingsu (40°23′N, 87°57′E) | A1 | 50 × 50 | 20 | 832 | 336 | 20 | 5.40 | 0.39 | 4.24 | 16.34 |
| A2 | 50 × 50 | 200 | 837 | 216 | 20 | 5.12 | 0.44 | 3.60 | 12.08 | |
| A3 | 50 × 50 | 400 | 826 | 316 | 20 | 5.39 | 0.22 | 3.28 | 9.53 | |
| A4 | 50 × 50 | 600 | 831 | 184 | 20 | 4.18 | 0.29 | 3.02 | 7.97 | |
| Arghan (40°08′N, 88°22′E) | B1 | 50 × 50 | 20 | 815 | 404 | 20 | 6.50 | 0.21 | 3.51 | 10.71 |
| B2 | 50 × 50 | 200 | 813 | 272 | 20 | 7.08 | 0.36 | 4.55 | 13.53 | |
| B3 | 50 × 50 | 400 | 818 | 292 | 20 | 6.12 | 0.30 | 4.26 | 15.78 | |
| B4 | 50 × 50 | 600 | 822 | 256 | 20 | 5.44 | 0.24 | 3.72 | 16.78 | |
| Iganbujima (39°47′N, 88°23′E) | C1 | 50 × 50 | 20 | 808 | 460 | 20 | 5.93 | 0.24 | 4.05 | 14.75 |
| C2 | 50 × 50 | 200 | 812 | 200 | 20 | 7.71 | 0.31 | 5.17 | 22.16 | |
| C3 | 50 × 50 | 400 | 803 | 152 | 20 | 4.78 | 0.37 | 3.61 | 13.14 | |
| C4 | 50 × 50 | 600 | 814 | 124 | 20 | 4.82 | 0.42 | 3.98 | 13.52 | |
The selection of sample trees considered two main factors. First, individual trees were completely scanned by TLS. Second, the trees with different growth conditions were selected. Because of mutual occlusion between the trees in the plots, TLS could not completely scan trunk structure of some trees. On the other hand, P. euphratica trees are phreatophytes and thus rely on groundwater to survive (Thomas and Lang, 2020). In the research area, with the increase of the distance from the river channel, the P. euphratica growth was affected by the decrease of the groundwater level and resulted in tree structural variability. The nonlinear relationship between tree height and DBH was changed in different distance from the river, the determination coefficient R2 decreased (Fig. 3). Therefore, we selected 240 trees (20 trees per plot) with different DBH classes and growth condition that were completely scanned by TLS as sample trees to measure the Vt in all plots (Fig. 4).
As shown in Fig. 5a, all sampled tree structural attributes were detailed and measured by TLS, and the point clouds were classified into tree and ground points, as well as the structural parameters of H, DBH, CD, CA, trunk height (TH), under branch height (BH), and basal diameter (BD) were acquired (Fig. 5b). High-precision TLS laser beams can scan crown intervals and reach the surface of trunks and branches to capture detailed point cloud RI data on tree structure. Lu et al. (2014) and Hackenberg et al. (2015) proposed that point cloud RI values of tree trunks and leaves were different. The point clouds of trees with lower RI values are mainly accounted to leaf points, while the higher RI values are accounted to the trunk points. Based on trial-and-error experiments (Lu et al., 2014), we manually selected the threshold of RI value, and found that the RI value below 70% on the histograms accounted to most part of the tree leaves and small branch points, and the RI value above 80% on the histograms accounted to the trunk and major branch points. Therefore, a threshold ranging from 70% to 80% of the RI value is determined to be applicable for extracting the points for most parts of the trunk. In this study, we set the threshold at 75% (Fig. 5c) and separated most of the leaves and trunks (Fig. 5d). The point clouds with intensities larger than the threshold constituted the major trunk of each tree (Fig. 5e).
The acquired trunk point clouds were processed to calculate the volume of each tree. The main idea of calculation algorithm is to split the trunk point clouds horizontally into layers at every 0.1 m from the bottom to the top of tree trunk height (TH), and applied the Hough transform method to obtain the trunk diameters (Di) of every layer automatically (Guo et al., 2018). In the volume algorithm, a trunk was split into multiple layers, which ensured that the irregular parts of tree trunks could be contained and calculated at high accuracy. Based on Di and TH values for 240 individual trees, the trunk curve line equation
|
Vt=TH∫0π[12f(Di)]2dDi |
(1) |
where Vt represents the trunk volume (m3); TH is the trunk height (m); π is the circle ratio; Di is the diameters of the trunk at the different height layers (m); i is the number of layers (
Owing to the difficulty in directly obtaining Vt in the field measurement to verify the calculated results of TLS data, the results were indirectly verified by other tree structure parameters based on the field measurement. We used a tree height altimeter (Blume-Leiss, Harbin Optical Instrument Factory Ltd, Heilongjiang, China), DBH rulers, and tape measures in each plot to measure 10 individual tree H, TH, BH, DBH, BD, CD, and CA. The liner regression analysis accuracy results had a high correlation, with a coefficient of determination (R2) ranging from 0.82 to 0.97 (P < 0.01) (Table 2). Therefore, the Vt obtained by TLS was taken as an accurate measurement value.
| Structural parameter |
TLS measured | Field measured | Standard deviation | R2 | RMSE | Sig. | |||
| range | Mean value | range | Mean value | ||||||
| H (m) | 2.19–11.14 | 7.46 | 3.80–14.10 | 7.25 | 1.65 | 0.95 | 0.32 | 0.01 | |
| TH (m) | 2.14–7.92 | 4.47 | 2.05–7.35 | 4.20 | 0.57 | 0.93 | 0.54 | 0.01 | |
| BH (m) | 0.94–5.23 | 2.25 | 1.10–5.30 | 2.30 | 0.64 | 0.90 | 0.72 | 0.01 | |
| DBH (cm) | 9.08–87.33 | 34.53 | 9.50–84.60 | 34.88 | 3.26 | 0.97 | 2.15 | 0.01 | |
| BD (cm) | 13.54–89.95 | 39.75 | 13.20–87.50 | 37.35 | 5.41 | 0.92 | 4.63 | 0.01 | |
| CD (m) | 1.54–7.92 | 5.02 | 1.25–7.50 | 5.52 | 0.73 | 0.89 | 0.58 | 0.01 | |
| CA (m2) | 1.87–49.21 | 20.74 | 1.19–47.90 | 23.30 | 2.82 | 0.87 | 4.77 | 0.01 | |
We selected 16 different trunk volume prediction functions (Meng, 2006; Li et al., 2020) that are commonly applied in forest surveys to establish the Vt estimation model, as shown in Table 3. Among these, the one-way volume table equations used DBH, the general volume table equations used DBH and H, and the three variable volume table equations used DBH, BD, H, and form quotient (q) parameters as explanatory variables. The structural parameters and Vt value data of 160 individual trees were inputted to each function, and a regression analysis was performed to acquire the fit statistics and model parameters using Stata (V13.0, Stata, Co. Ltd.).
| Regression models | Equation | No. |
| One-way volume table equations | (1) | |
| (2) | ||
| (3) | ||
| (4) | ||
| (5) | ||
| (6) | ||
| General volume table equations | (7) | |
| (8) | ||
| (9) | ||
| (10) | ||
| (11) | ||
| (12) | ||
| (13) | ||
| Three variable volume table equations | (14) | |
| (15) | ||
| (16) | ||
| Note: Vt is trunk volume (m3) |
||
To evaluate the goodness of model fit, the statistical parameters RMSE, R2, and the Bayesian information criterion (BIC) were calculated, and the best prediction model was selected. The calculation formula was as follows:
|
BIC=nlnn∑i=1(yi−ˆyi)2−nlnn+(lnn)p |
(2) |
where n is the number of samples, p is the number of parameters,
To test the model prediction accuracy, structural parameter data for 80 individual trees was used to calculate the Vt values, and the linear regression fitting was performed with the TLS-measured Vt to obtain the model accuracy. The mean prediction error (ME), mean absolute error (MAE), and modeling efficiency (EF) values were used to compare the model prediction ability. The specific calculation formula was as follows:
|
ME=n∑i=1(yi−ˆyin) |
(3) |
|
MAE=1nn∑i=1|yi−ˆyiyi|×100 |
(4) |
|
EF=1−n∑i=1(yi−ˆyi)2/(yi−ˉyi)2 |
(5) |
The model with lower ME, MAE, and higher EF values had a higher prediction accuracy. To further test the model application, we also assessed model accuracy by comparing it with existing Vt prediction models for P. euphratica proposed by Dong et al. (2013) and Huang et al. (2018), as shown in Table 4.
| Presenter | Model | Predicted index | Change of independent variable |
| Dong et al. (2013) | Trunk volume | H = 8.20–10.00 m, DBH = 22.00–25.00 cm |
|
| Huang et al. (2018) | Trunk volume | H = 3.00–9.50 m, DBH = 8.00–70.00 cm |
|
| Note: Vt, trunk volume (m3); DBH, diameter at breast height (m); H, tree height (m); BD, basal trunk diameter (m). | |||
TLS-acquired Vt for P. euphratica trees of different H ranged from 0.03 to 1.56 m3 in the study plots (Fig. 6a). For 97% of the sampled trees, Vt were less than 0.8 m3; few trees had a Vt greater than 0.8 m3. However, the Vt of these trees were obviously different, even at the same H level. There was no significant correlation between H and Vt (R2 = 0.11, P < 0.01), and many trees had irregularly shaped trunks. As H increased, the tree Vt showed an obviously scattered distribution, especially above the 7 m range (Fig. 6b). The trees with H of less than 5 m had similar Vt. As the H of P. euphratica increased, the trunk shapes showed more irregularity in the study area.
The fitted results of all candidate models for P. euphratica Vt are presented in Table 5. All models were examined and evaluated based on multiple model performance criteria. The one-way volume models (1–6) that used DBH as the independent variable had relatively high accuracy, with a determination coefficient R2 in range of 0.85–0.91 (P < 0.01); among these models, the model 3, 4, and 6 had relatively higher BIC values, which indicated a better degree of fit. The general volume models (7–13) that used different conversion forms of DBH and H as independent variables had higher accuracy than the one-way volume equations models, the R2 values were in the range of 0.90–0.94 (P < 0.01). Models 10 and 12 had relatively higher BIC values and passed the t-test, which indicated a better degree of fit. The three variable equations models (14–16) showed the highest accuracy, the R2 values were in the range of 0.93–0.96 (P < 0.01). Among these, models 14 and 16 had the highest BIC and F values. This indicates that H, DBH, BD, and q were the most effective independent variables to predict the Vt of the trees. Among all the volume models, the three-variable equation model 14 had the highest determination coefficient and BIC value, and the regression equation passed the F-test and t-test for significance.
| Equations | Models | Parameter estimation value | Statistical index | ||||||||||||
| SSE | SSR | RMSE | F | t | P > |t| | R2 | BIC | ||||||||
| One-way volume table equations | (1) | 0.036 | 2.401 | 7.53 | 0.87 | 0.087 | 989.85 | 31.46 | 0.00 | 0.896 | ‒311.47 | ||||
| (2) | ‒0.103 | 0.766 | 1.502 | 7.60 | 0.80 | 0.084 | 539.81 | 3.20 | 0.00 | 0.905 | ‒305.59 | ||||
| (3) | 2.671 | 1.991 | 68.90 | 5.25 | 0.214 | 1508.70 | 38.84 | 0.00 | 0.929 | ‒52.43 | |||||
| (4) | 0.900 | 1.627 | ‒0.099 | 69.11 | 5.04 | 0.210 | 781.15 | 9.28 | 0.00 | 0.931 | ‒47.31 | ||||
| (5) | 0.131 | 5.479 | 7.16 | 1.24 | 0.104 | 663.99 | 25.77 | 0.00 | 0.852 | ‒317.30 | |||||
| (6) | 6.686 | 2.406 | 0.274 | 69.14 | 5.01 | 0.210 | 786.55 | 13.08 | 0.00 | 0.932 | ‒47.25 | ||||
| General volume table equations | (7) | ‒0.178 | 1.951 | ‒2.630 | ‒0.091 | 0.451 | 7.97 | 0.43 | 0.062 | 520.77 | 4.33 | 0.01 | 0.949 | ‒290.45 | |
| (8) | 0.202 | 1.474 | ‒0.028 | ‒0.043 | 0.015 | 7.95 | 0.46 | 0.064 | 486.73 | 4.37 | 0.13 | 0.945 | ‒290.86 | ||
| (9) | 2.336 | 1.868 | 0.035 | 1.777 | 70.14 | 4.01 | 0.188 | 658.31 | 37.44 | 0.01 | 0.946 | ‒40.82 | |||
| (10) | 0.860 | 1.870 | 0.509 | 70.13 | 4.02 | 0.187 | 994.10 | 37.74 | 0.00 | 0.946 | ‒45.59 | ||||
| (11) | 0.061 | 0.293 | 7.81 | 0.59 | 0.072 | 1521.90 | 39.01 | 0.00 | 0.929 | ‒307.13 | |||||
| (12) | 0.008 | 7.343 | 0.745 | 67.03 | 7.12 | 0.250 | 536.51 | 27.47 | 0.00 | 0.904 | ‒50.88 | ||||
| (13) | ‒0.009 | 1.629 | ‒0.234 | 0.261 | 0.135 | 13.24 | 0.75 | 0.082 | 495.24 | 8.02 | 0.00 | 0.947 | ‒231.14 | ||
| Three variables volume table equations |
(14) | 0.909 | 1.184 | 0.487 | 0.836 | 71.88 | 2.28 | 0.141 | 1188.52 | 14.32 | 0.00 | 0.969 | ‒37.96 | ||
| (15) | ‒0.101 | 0.128 | 0.500 | ‒0.172 | 7.85 | 0.55 | 0.069 | 535.25 | 5.74 | 0.01 | 0.933 | ‒297.04 | |||
| (16) | 0.889 | 1.994 | 0.489 | 0.743 | 71.50 | 2.65 | 0.153 | 1014.8 | 45.77 | 0.00 | 0.950 | ‒38.57 | |||
According to the Vt regression model estimation results, the candidate estimation models 3, 4, 6, 9, 10, 12, 14, and 16 had a good fit, R2 > 0.9, and low BIC values. To further test the model prediction accuracy of these eight models, the deviation statistical parameters were compared, as shown in Table 6. Among them, model 14 had the lowest ME and MAE and highest EF values.
| Model | ME | MAE | EF | F | Sig |
| (3) | 0.015 | 2.463 | 0.933 | 31.037 | 0.002 |
| (4) | 0.016 | 1.434 | 0.948 | 26.910 | 0.003 |
| (6) | 0.015 | 1.558 | 0.946 | 25.559 | 0.003 |
| (9) | 0.006 | 3.019 | 0.957 | 35.763 | 0.002 |
| (10) | 0.007 | 3.212 | 0.958 | 35.762 | 0.002 |
| (12) | 0.011 | 15.007 | 0.943 | 34.082 | 0.002 |
| (14) | 0.006 | 1.177 | 0.961 | 39.089 | 0.001 |
| (16) | 0.065 | 24.381 | 0.875 | 37.59 | 0.001 |
Therefore, model 14 was the optimal Vt estimation model for P. euphratica tree:
|
Vt=0.909DBH1.184×H0.487×BD0.836 |
The structural parameters of 80 sample trees, which included H, DBH, BD, and Vt obtained by TLS, were used to test the estimation model accuracy. The model-predicted Vt and TLS-acquired Vt values were highly consistent, the R2 was 0.92 (P ≤ 0.01), and the RMSE was 0.046 m3 (Fig. 7). Compared with existing Vt prediction models (Table 4), the model-predicted trends were basically consistent (Fig. 8), and Vt < 0.5 m3 showed no obvious difference; however, the prediction trends of different models varied with increasing Vt. The maximum Vt predicted by each model differed greatly. The results of our model were in good agreement with the reference line. This indicated that the Vt prediction model had reliable accuracy.
Research interest in measuring and estimating forest biomass and carbon stock has increased due to the United Nations Framework Convention on Climate Change and China Carbon Neutrality Policy (Pretzsch, 2009; Piao et al., 2011; Cosmo et al., 2016; Saarinen et al., 2017). In Central Asia, the P. euphratica riparian forest has the highest aboveground biomass and carbon sequestration (Thevs et al., 2012). Along the Tarim River, P. euphratica forest has undergone 20-year ecological engineering projects, including artificial water diversion and embankment measures (Xu et al., 2007; Zeng et al., 2009). Regarding climate change mitigation, riparian forest restoration can be traded on the international carbon market (Buras et al., 2013; Aishan et al., 2018). The quantification of the forest stand volumes and biomass provides essential information for evaluating carbon sequestration ability and the effects of manmade restoration projects on the productivity of this arid riparian forest ecosystem. Tree Vt is one of the most basic parameters for estimating stand volume and biomass. Dong et al. (2013) and Wang et al. (2016) acquired the P. euphratica biomass using tree volume and average wood density values, and fitted a model for the relationship between tree volume and biomass along the Tarim River. Therefore, high-precision measurement of tree volume is an important task in the forest survey. Wang et al. (2003) developed tree growth pattern equations and acquired data on the bio-productivity and biomass of P. euphratica trees by the harvested sample trees in the Ejina Basin, and found that the trunk biomass has the largest proportion, accounting for 36%–61% of total tree biomass. With the increase of the distance from the river, the groundwater level decreased, and the P. euphratica growth status was changed in the different site conditions, particularly the allometric relationship between H and DBH was not consistent. Therefore, the trunk volume and biomass proportion were affected by the tree growth structure. However, traditional allometric equations for estimating biomass are difficult to detect this structural variability. The point cloud data acquired by LiDAR generates 3D models of trees enabling us to avoid the volume estimation uncertainty caused by changes in the growth structure.
Data collection for traditional field measurement of Vt is challenging because of its destructiveness, insufficient sample size, and time requirements (Li et al., 2020; Zuleta et al., 2022), which make it impractical for such a highly protected species such as P. euphratica (Huang et al., 2018). Therefore, it is necessary to adopt a nondestructive method to measure the Vt of P. euphratica forests.
LiDAR technology has obvious advantages in presenting 3D information for forest inventories and has demonstrated the ability to estimate forest structure and related parameters such as tree volume (Zimble et al., 2003; Brede et al., 2019; Wiggins et al., 2019). The accuracy of tree volume estimation using LiDAR point cloud data may differ among trees due to species-specific differences in tree architecture (Vicari et al., 2019). Most studies have used a voxel-based bounding method based on the topological attributes of tree point cloud data to reconstruct tree structure models and calculate tree volume or other attributes (Kukkonen et al., 2021; Zuleta et al., 2022). These methods are most suitable for tree species with regular growth structures, such as pine, spruce, and beech, where tree architectural shapes are basically similar and measuring the trunk diameters at the same tree height does not lead to high uncertainty. As shown in Fig. 3, in the research area of Tarim River lower reaches, with the increase of distance from the river channel, the nonlinear relationship between the P. euphratica tree height and DBH exhibited differences, and correlation coefficient has decreased. Therefore, the nonlinear relationship between the basic structural parameters of trees can reflect the regular and irregular shaped trees to some extent. Point clouds can also be used to effectively reconstruct the steam models. However, irregularly shaped tree architectural complexity hinders the application of voxel-based methods (Hess et al., 2015; Bauwens et al., 2021). Therefore, it is necessary to find other methods to extract tree structure data. Hackenberg et al. (2015) predicted the aboveground leafless biomass of deciduous trees using point cloud RI data. Lu et al. (2014) found that the intensity of trunk point clouds differs from that of other parts of the tree, and this characteristic of LiDAR data can segment individual trees in deciduous forests with high accuracy. The LiDAR product multiple returning pulses, the total energy for each pulse emitted from the sensor was the same no matter how many total echoes it had. For the same texture surface conditions, the RI energy allocated to each echo is less for a pulse that has more total echoes than for a pulse that has fewer echoes. The points for leaves and small branches, which have fewer total echoes than those for tree trunks, may have larger RI values (Lu et al., 2014). These studies showed that RI also has an advantage in tree trunk and leaf segmentation. In the present study, the P. euphratica forest observation data showed an irregularly shaped trunk growth status in the research area (Fig. 3), and it was difficult to obtain the trunk volume accurately by traditional allometric monitoring methods. Therefore, we used the TLS point cloud RI data to separate the major part of the trunks and leaves of trees (Fig. 5c). The results showed that the intensity threshold accurately obtained the major part of the P. euphratica tree trunk, as shown in Table 2. This approach is simple to implement and suitable for obtaining the Vt of trees under different growth conditions.
Most of the candidate models (Table 5) performed quite well at delineating the relationship between tree Vt and structural attributes for the P. euphratica riparian forest. Based on the analysis of the multi model performance criteria, we found that models 10, 12, 14, and 16 were more effective at predicting tree Vt compared to other candidate models. Among them, three variable model 14 provided the most satisfactory Vt estimates. Considering all model performance criteria, we selected model 14 as a potential best model because it performed best across the general volume models. The three variable models were more effective than the general model at predicting the Vt of P. euphratica trees because the shape of trunks showed irregularity under the long-term drought environmental conditions along the lower Tarim River.
Previous studies have mainly used harvest methods to estimate P. euphratica volume and biomass. Li et al. (1994) investigated the regularities of tree volume growth using felled sample trees and found that the mature tree volume was 0.329–0.366 m3, which was consistent with our results (Fig. 7). Wang et al. (2016) used destructive sampling of 40 young trees to acquire whole individual tree biomass and adopted tree volume to develop a biomass estimation model. However, in their study, tree trunk shape was regarded as a cylinder and the crown was regarded as a cone, which might lead to uncertainty in the volume prediction accuracy of the model. Previous studies have provided a good basis for estimating P. euphratica tree volume based on traditional field measurements. However, using the destructive method makes it difficult in acquiring a wide range of data, thereby limiting the practicality and accuracy of prediction models. Huang et al. (2018) used a 3D scanning smartphone application to obtain the Vt of P. euphratica trees nondestructively and detected a volume of 91 trees, which were distributed near the riverbank. When collecting model training parameters, the population characteristic changes in P. euphratica at different distances from a river must be considered to improve the model's availability. In the lower reaches of the Tarim River, P. euphratica trees mainly spread along the river channel on both sides in a 2-km range (Zhang et al., 2013; Mamat et al., 2019), and with increasing vertical distance to the river, stand density declines and tree growth conditions change (Thevs et al., 2012; Thomas et al., 2016; Keyimu et al., 2017b; Keyimu et al., 2018). Therefore, we set up 12 plots within 600 m of the river channel at three sections along the lower Tarim River and acquired tree structural information for trees of different ages, as shown in Table 1 and Fig. 4, which improved the fitness accuracy of the prediction models in this region. According to existing models proposed by Dong et al. (2013) and Huang et al. (2018), all models prediction results of Vt for small trees were consistent, but for the high trees were different, as shown in Fig. 8. This is because, as the increase of distance from the river, most of the small trees do not have obvious irregularly shaped trunks, and the Vt value variation was small. However, for the high trees the relationships between the H and DBH are more dispersed under different site conditions (Fig. 3), which led to wide variation in Vt (Fig. 6). Therefore, our prediction model has a certain difference in the predicted results for high trees (Fig. 8). The previous models were built mainly using two attributes of H and DBH, and did not account for other morphological variables such as trunk shape. In the present study, the participation of independent variables of BD and DBH can better predict the Vt, and the combination of variable H has reflected the general change trend of trunk shape, as well as improved the estimation accuracy of the model. Additionally, for the trees in the desert riparian areas, the mathematical relationship of the model developed in this study can be applied to the other species such as Populus pruinose and Elaeagnus angustifolia trees in the riparian areas, which share similar growth structure to P. euphratica, and improve the traditional allometric growth models estimation accuracy.
High-precision TLS point clouds RI data can acquire the irregular trunk structure of P. euphratica trees. This method nondestructively measures the trunk volume of irregularly shaped trees and can improve traditional forest inventory, as well as providing an accurate database for constructing regression models. Fitting of 16 models to predict Vt showed that the three variable models had more accurate predictability compared to the one-way and general volume models. Among them, tree structural attributes of H, DBH, and BD as variables of the prediction model had the highest estimation accuracy. Compared to the previous models, adding BD and trunk form factor, which are conveniently acquired attributes, will improve the model prediction capability for irregularly shaped P. euphratica Vt. The results provide an essential basis for accurately estimating the forest stock, growth, biomass, and carbon storage of desert riparian forests, which will improve our understanding of regional riparian forest dynamics over time as an effect of ecological restoration measures conducted in the region.
AY and ÜH conceived, designed, and performed the experiments, collected, and analyzed the data, prepared figures, and tables, and wrote the manuscript draft. MK, TA, AA, BD and JW participated in field work and contributed to data collection, analysis, and the manuscript writing. All authors checked and approved the final content of the manuscript.
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Special thanks to Xinjiang LiDAR Applied Engineering Technology Center for renting the Riegl VZ-1000 TLS equipment. We also would like to express our gratitude to the editors and reviewers for their helpful comments and careful revision of this manuscript.
| Section | Plots | Area (m2) | Distance from the river (m) | Altitude (m) | Tree density (trees·ha−1) | Sampled trees | Mean values of tree structural attributes | |||
| H (m) | DBH (m) | CD (m) | CA (m2) | |||||||
| Yingsu (40°23′N, 87°57′E) | A1 | 50 × 50 | 20 | 832 | 336 | 20 | 5.40 | 0.39 | 4.24 | 16.34 |
| A2 | 50 × 50 | 200 | 837 | 216 | 20 | 5.12 | 0.44 | 3.60 | 12.08 | |
| A3 | 50 × 50 | 400 | 826 | 316 | 20 | 5.39 | 0.22 | 3.28 | 9.53 | |
| A4 | 50 × 50 | 600 | 831 | 184 | 20 | 4.18 | 0.29 | 3.02 | 7.97 | |
| Arghan (40°08′N, 88°22′E) | B1 | 50 × 50 | 20 | 815 | 404 | 20 | 6.50 | 0.21 | 3.51 | 10.71 |
| B2 | 50 × 50 | 200 | 813 | 272 | 20 | 7.08 | 0.36 | 4.55 | 13.53 | |
| B3 | 50 × 50 | 400 | 818 | 292 | 20 | 6.12 | 0.30 | 4.26 | 15.78 | |
| B4 | 50 × 50 | 600 | 822 | 256 | 20 | 5.44 | 0.24 | 3.72 | 16.78 | |
| Iganbujima (39°47′N, 88°23′E) | C1 | 50 × 50 | 20 | 808 | 460 | 20 | 5.93 | 0.24 | 4.05 | 14.75 |
| C2 | 50 × 50 | 200 | 812 | 200 | 20 | 7.71 | 0.31 | 5.17 | 22.16 | |
| C3 | 50 × 50 | 400 | 803 | 152 | 20 | 4.78 | 0.37 | 3.61 | 13.14 | |
| C4 | 50 × 50 | 600 | 814 | 124 | 20 | 4.82 | 0.42 | 3.98 | 13.52 | |
| Structural parameter |
TLS measured | Field measured | Standard deviation | R2 | RMSE | Sig. | |||
| range | Mean value | range | Mean value | ||||||
| H (m) | 2.19–11.14 | 7.46 | 3.80–14.10 | 7.25 | 1.65 | 0.95 | 0.32 | 0.01 | |
| TH (m) | 2.14–7.92 | 4.47 | 2.05–7.35 | 4.20 | 0.57 | 0.93 | 0.54 | 0.01 | |
| BH (m) | 0.94–5.23 | 2.25 | 1.10–5.30 | 2.30 | 0.64 | 0.90 | 0.72 | 0.01 | |
| DBH (cm) | 9.08–87.33 | 34.53 | 9.50–84.60 | 34.88 | 3.26 | 0.97 | 2.15 | 0.01 | |
| BD (cm) | 13.54–89.95 | 39.75 | 13.20–87.50 | 37.35 | 5.41 | 0.92 | 4.63 | 0.01 | |
| CD (m) | 1.54–7.92 | 5.02 | 1.25–7.50 | 5.52 | 0.73 | 0.89 | 0.58 | 0.01 | |
| CA (m2) | 1.87–49.21 | 20.74 | 1.19–47.90 | 23.30 | 2.82 | 0.87 | 4.77 | 0.01 | |
| Regression models | Equation | No. |
| One-way volume table equations | (1) | |
| (2) | ||
| (3) | ||
| (4) | ||
| (5) | ||
| (6) | ||
| General volume table equations | (7) | |
| (8) | ||
| (9) | ||
| (10) | ||
| (11) | ||
| (12) | ||
| (13) | ||
| Three variable volume table equations | (14) | |
| (15) | ||
| (16) | ||
| Note: Vt is trunk volume (m3) |
||
| Presenter | Model | Predicted index | Change of independent variable |
| Dong et al. (2013) | Trunk volume | H = 8.20–10.00 m, DBH = 22.00–25.00 cm |
|
| Huang et al. (2018) | Trunk volume | H = 3.00–9.50 m, DBH = 8.00–70.00 cm |
|
| Note: Vt, trunk volume (m3); DBH, diameter at breast height (m); H, tree height (m); BD, basal trunk diameter (m). | |||
| Equations | Models | Parameter estimation value | Statistical index | ||||||||||||
| SSE | SSR | RMSE | F | t | P > |t| | R2 | BIC | ||||||||
| One-way volume table equations | (1) | 0.036 | 2.401 | 7.53 | 0.87 | 0.087 | 989.85 | 31.46 | 0.00 | 0.896 | ‒311.47 | ||||
| (2) | ‒0.103 | 0.766 | 1.502 | 7.60 | 0.80 | 0.084 | 539.81 | 3.20 | 0.00 | 0.905 | ‒305.59 | ||||
| (3) | 2.671 | 1.991 | 68.90 | 5.25 | 0.214 | 1508.70 | 38.84 | 0.00 | 0.929 | ‒52.43 | |||||
| (4) | 0.900 | 1.627 | ‒0.099 | 69.11 | 5.04 | 0.210 | 781.15 | 9.28 | 0.00 | 0.931 | ‒47.31 | ||||
| (5) | 0.131 | 5.479 | 7.16 | 1.24 | 0.104 | 663.99 | 25.77 | 0.00 | 0.852 | ‒317.30 | |||||
| (6) | 6.686 | 2.406 | 0.274 | 69.14 | 5.01 | 0.210 | 786.55 | 13.08 | 0.00 | 0.932 | ‒47.25 | ||||
| General volume table equations | (7) | ‒0.178 | 1.951 | ‒2.630 | ‒0.091 | 0.451 | 7.97 | 0.43 | 0.062 | 520.77 | 4.33 | 0.01 | 0.949 | ‒290.45 | |
| (8) | 0.202 | 1.474 | ‒0.028 | ‒0.043 | 0.015 | 7.95 | 0.46 | 0.064 | 486.73 | 4.37 | 0.13 | 0.945 | ‒290.86 | ||
| (9) | 2.336 | 1.868 | 0.035 | 1.777 | 70.14 | 4.01 | 0.188 | 658.31 | 37.44 | 0.01 | 0.946 | ‒40.82 | |||
| (10) | 0.860 | 1.870 | 0.509 | 70.13 | 4.02 | 0.187 | 994.10 | 37.74 | 0.00 | 0.946 | ‒45.59 | ||||
| (11) | 0.061 | 0.293 | 7.81 | 0.59 | 0.072 | 1521.90 | 39.01 | 0.00 | 0.929 | ‒307.13 | |||||
| (12) | 0.008 | 7.343 | 0.745 | 67.03 | 7.12 | 0.250 | 536.51 | 27.47 | 0.00 | 0.904 | ‒50.88 | ||||
| (13) | ‒0.009 | 1.629 | ‒0.234 | 0.261 | 0.135 | 13.24 | 0.75 | 0.082 | 495.24 | 8.02 | 0.00 | 0.947 | ‒231.14 | ||
| Three variables volume table equations |
(14) | 0.909 | 1.184 | 0.487 | 0.836 | 71.88 | 2.28 | 0.141 | 1188.52 | 14.32 | 0.00 | 0.969 | ‒37.96 | ||
| (15) | ‒0.101 | 0.128 | 0.500 | ‒0.172 | 7.85 | 0.55 | 0.069 | 535.25 | 5.74 | 0.01 | 0.933 | ‒297.04 | |||
| (16) | 0.889 | 1.994 | 0.489 | 0.743 | 71.50 | 2.65 | 0.153 | 1014.8 | 45.77 | 0.00 | 0.950 | ‒38.57 | |||
| Model | ME | MAE | EF | F | Sig |
| (3) | 0.015 | 2.463 | 0.933 | 31.037 | 0.002 |
| (4) | 0.016 | 1.434 | 0.948 | 26.910 | 0.003 |
| (6) | 0.015 | 1.558 | 0.946 | 25.559 | 0.003 |
| (9) | 0.006 | 3.019 | 0.957 | 35.763 | 0.002 |
| (10) | 0.007 | 3.212 | 0.958 | 35.762 | 0.002 |
| (12) | 0.011 | 15.007 | 0.943 | 34.082 | 0.002 |
| (14) | 0.006 | 1.177 | 0.961 | 39.089 | 0.001 |
| (16) | 0.065 | 24.381 | 0.875 | 37.59 | 0.001 |